Datasets:
id
int64 1
18.1k
| prompt
stringlengths 2.24k
72.3k
| ground-truth rule
stringlengths 59
649
| validation program
stringlengths 316
69.3k
| symbols
stringlengths 51
11.8k
| curriculum level
int64 1
20
| curriculum tier
stringclasses 4
values | rule sampling
stringclasses 2
values | rule complexity
stringclasses 6
values | background sampling
stringclasses 2
values | problem size
int64 2
32
| vocabulary predicates
int64 5
12
| vocabulary car constants
stringclasses 6
values |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
1 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est -29 1 blanc court complet
ouest 172 1 jaune court complet
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
2 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est 227 1 blanc court rampe
ouest -6 1 jaune court rampe
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
3 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 19 1 bleu long complet
ouest -39 1 bleu court complet
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
4 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
|
est -50 1 blanc long complet
ouest -21 1 rouge long complet
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
5 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 129 1 vert long complet
ouest 51 1 vert court complet
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
6 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
|
est 36 1 blanc long complet
ouest 167 1 jaune long complet
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
7 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 48 1 blanc long complet
ouest 22 1 blanc court complet
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
8 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est -17 1 vert long rampe
ouest 135 1 vert court rampe
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
9 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
|
est 211 1 blanc long complet
ouest 198 1 vert long complet
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
10 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est 185 1 rouge long rampe
ouest 34 1 rouge court rampe
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
11 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 230 1 blanc court complet
ouest 188 1 bleu court complet
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
12 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est -53 1 bleu long rampe
ouest 235 1 bleu court rampe
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
13 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
|
est 121 1 blanc long complet
ouest -51 1 bleu long complet
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
14 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 22 1 rouge long complet
ouest -30 1 rouge court complet
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
15 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, jaune).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, jaune).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est 223 1 jaune long rampe
ouest 13 1 jaune court rampe
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
16 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est -60 1 blanc court complet
ouest 229 1 rouge court complet
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
17 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
|
est 130 1 blanc long rampe
ouest 11 1 jaune long rampe
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
18 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, jaune).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, jaune).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est -17 1 jaune long complet
ouest 190 1 jaune court complet
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
19 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
|
est 28 1 blanc long rampe
ouest 20 1 vert long rampe
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
20 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est 235 1 blanc long rampe
ouest 169 1 blanc court rampe
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
21 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
|
est 7 1 blanc long rampe
ouest 26 1 bleu long rampe
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
22 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est 130 1 blanc court rampe
ouest 147 1 vert court rampe
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
23 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 201 1 blanc court complet
ouest 60 1 vert court complet
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
24 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est 172 1 blanc court rampe
ouest 144 1 bleu court rampe
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
25 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
|
est 2 1 blanc long rampe
ouest 54 1 rouge long rampe
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
26 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est -54 1 blanc court rampe
ouest 226 1 rouge court rampe
| 1 |
basic
|
random
|
1
|
mirror
| 2 | 5 |
1
|
27 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, jaune).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, jaune), a_paroi(Wagon1, complet).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, jaune).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
|
est 193 1 jaune long complet
ouest -1 1 rouge long rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
28 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, bleu), a_wagon(Train, Wagon2), longueur_wagon(Wagon2, court).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
|
est -59 1 bleu court rampe
ouest 159 1 rouge long rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
29 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), a_paroi(Wagon1, rampe), a_wagon(Train, Wagon2), couleur_wagon(Wagon2, vert).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 199 1 vert court rampe
ouest 40 1 blanc court complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
30 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 179 1 bleu long complet
ouest 133 1 bleu court complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
31 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), a_paroi(Wagon1, complet), a_wagon(Train, Wagon2), couleur_wagon(Wagon2, rouge).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est 150 1 rouge court complet
ouest 167 1 blanc court rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
32 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long), couleur_wagon(Wagon1, rouge).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est 60 1 rouge long rampe
ouest 160 1 blanc court rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
33 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), a_paroi(Wagon1, complet), a_wagon(Train, Wagon2), longueur_wagon(Wagon2, court).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
|
est -34 1 bleu court complet
ouest 173 1 bleu long rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
34 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, vert), numero_wagon(Wagon1, 1).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
|
est 55 1 vert long rampe
ouest 186 1 rouge long rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
35 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), a_paroi(Wagon1, complet), a_wagon(Train, Wagon2), couleur_wagon(Wagon2, vert).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
|
est 217 1 vert long complet
ouest 54 1 blanc long rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
36 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long), a_paroi(Wagon1, rampe).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 180 1 rouge long rampe
ouest -58 1 rouge court complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
37 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long), a_wagon(Train, Wagon2), a_paroi(Wagon2, complet).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est -50 1 vert long complet
ouest 169 1 vert court rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
38 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, jaune).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, court), couleur_wagon(Wagon1, jaune).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, jaune).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
|
est 143 1 jaune court rampe
ouest 180 1 vert long rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
39 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, jaune).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, jaune), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, jaune).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 155 1 jaune long complet
ouest -33 1 bleu court complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
40 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, bleu), a_wagon(Train, Wagon2), longueur_wagon(Wagon2, court).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
|
est -9 1 bleu court complet
ouest -20 1 blanc long complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
41 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, jaune).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, jaune).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 174 1 jaune long complet
ouest 203 1 jaune court complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
42 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), a_paroi(Wagon1, complet), a_wagon(Train, Wagon2), couleur_wagon(Wagon2, bleu).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est 124 1 bleu court complet
ouest 231 1 rouge court rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
43 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
|
est 129 1 blanc long complet
ouest 138 1 jaune long complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
44 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, jaune).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), a_paroi(Wagon1, rampe), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, jaune).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 162 1 jaune long rampe
ouest 146 1 jaune court complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
45 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long), a_wagon(Train, Wagon2), couleur_wagon(Wagon2, vert).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est -7 1 vert long rampe
ouest 40 1 blanc court rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
46 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, court), a_wagon(Train, Wagon2), a_paroi(Wagon2, rampe).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
|
est 37 1 rouge court rampe
ouest 138 1 rouge long complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
47 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, vert), a_wagon(Train, Wagon2), longueur_wagon(Wagon2, court).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
|
est 202 1 vert court complet
ouest 183 1 jaune long complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
48 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 178 1 rouge long complet
ouest 21 1 rouge court complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
49 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), a_paroi(Wagon1, complet), a_wagon(Train, Wagon2), longueur_wagon(Wagon2, court).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
|
est 27 1 vert court complet
ouest 19 1 vert long rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
50 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
|
est 220 1 blanc long rampe
ouest 11 1 rouge long rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
51 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, court), a_wagon(Train, Wagon2), longueur_wagon(Wagon2, court).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, bleu).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
|
est -59 1 bleu court complet
ouest -29 1 bleu long complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
52 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est 25 1 blanc long rampe
ouest -40 1 blanc court rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
53 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 35 1 blanc long complet
ouest 197 1 blanc court complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
54 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), a_paroi(Wagon1, rampe), a_wagon(Train, Wagon2), couleur_wagon(Wagon2, bleu).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est -15 1 bleu court rampe
ouest 55 1 rouge court complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
55 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc), a_wagon(Train, Wagon2), a_paroi(Wagon2, complet).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
|
est 146 1 blanc long complet
ouest 134 1 jaune long rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
56 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, bleu), a_wagon(Train, Wagon2), longueur_wagon(Wagon2, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 180 1 bleu long complet
ouest 48 1 jaune court complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
57 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, bleu), a_wagon(Train, Wagon2), longueur_wagon(Wagon2, court).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, bleu).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, rampe).
|
est 146 1 bleu court rampe
ouest -50 1 jaune long rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
58 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long), a_wagon(Train, Wagon2), couleur_wagon(Wagon2, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 198 1 blanc long complet
ouest 187 1 rouge court complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
59 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), a_paroi(Wagon1, rampe), couleur_wagon(Wagon1, rouge).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, vert).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
|
est 7 1 rouge long rampe
ouest 220 1 vert long complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
60 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, rouge).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est 28 1 rouge long rampe
ouest 167 1 rouge court rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
61 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, rouge).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, complet).
|
est 159 1 blanc court complet
ouest 208 1 rouge court complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
62 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), couleur_wagon(Wagon1, vert), a_wagon(Train, Wagon2), longueur_wagon(Wagon2, court).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, vert).
longueur_wagon(wagon0_1, court).
a_paroi(wagon0_1, complet).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, blanc).
longueur_wagon(wagon1_1, long).
a_paroi(wagon1_1, complet).
|
est 237 1 vert court complet
ouest 168 1 blanc long complet
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
63 |
Vous êtes un classificateur de trains qui observe des trains se déplaçant soit vers l'est soit vers l'ouest.
Chaque train est composé d'un ou plusieurs wagons, et chaque wagon est caractérisé par un ensemble de propriétés, représentées comme des atomes de base sur un ensemble fixe de prédicats.
La direction (vers l'est ou vers l'ouest) d'un train doit être déterminée à partir de sa composition.
Pour décrire les trains, nous définissons un ensemble de prédicats et de domaines de base :
- 'a_wagon(Train, Wagon)' : Indique que 'Wagon' fait partie du train 'Train'.
- 'numero_wagon(Wagon, Numero)' : Indique la position du wagon dans son train. 'Numero' est un entier positif.
- 'couleur_wagon(Wagon, Couleur)' : Indique la couleur du wagon. 'Couleur' peut être 'rouge', 'bleu', 'vert', 'jaune' ou 'blanc'.
- 'longueur_wagon(Wagon, Longueur)' : Indique la longueur du wagon. 'Longueur' peut être 'court' ou 'long'.
- 'a_paroi(Wagon, TypeParoi)' : Indique le type de paroi d'un wagon. 'TypeParoi' peut être 'complet' ou 'rampe'.
Vous disposez d'exemples positifs et négatifs sous la forme est(t) ou ouest(t) pour chaque train t, ainsi que de faits de base décrivant sa composition sur les prédicats ci-dessus.
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
Votre tâche consiste à formuler une hypothèse sous la forme d'une règle Prolog „est(T) :- Corps.“ qui distingue correctement les trains se dirigeant vers l'est de ceux se dirigeant vers l'ouest.
L'hypothèse doit être vraie pour tous les exemples positifs (c'est-à-dire les trains étiquetés est(t)) et fausse pour tous les exemples négatifs (c'est-à-dire les trains ouest(t)).
L'objectif est de trouver la règle correcte la plus courte, c'est-à-dire celle qui utilise le nombre minimal de littéraux dans le corps sans perdre de conditions nécessaires.
Votre règle ne peut utiliser que les prédicats définis dans l'ouverture ci-dessus et doit parfaitement séparer les trains vers l'est des trains vers l'ouest.
|
est(Train):- a_wagon(Train, Wagon1), longueur_wagon(Wagon1, long), a_wagon(Train, Wagon2), couleur_wagon(Wagon2, blanc).
|
est(train0).
a_wagon(train0, wagon0_1).
numero_wagon(wagon0_1, 1).
couleur_wagon(wagon0_1, blanc).
longueur_wagon(wagon0_1, long).
a_paroi(wagon0_1, rampe).
ouest(train1).
a_wagon(train1, wagon1_1).
numero_wagon(wagon1_1, 1).
couleur_wagon(wagon1_1, jaune).
longueur_wagon(wagon1_1, court).
a_paroi(wagon1_1, rampe).
|
est -16 1 blanc long rampe
ouest 152 1 jaune court rampe
| 2 |
basic
|
random
|
1-2
|
mirror
| 2 | 5 |
1
|
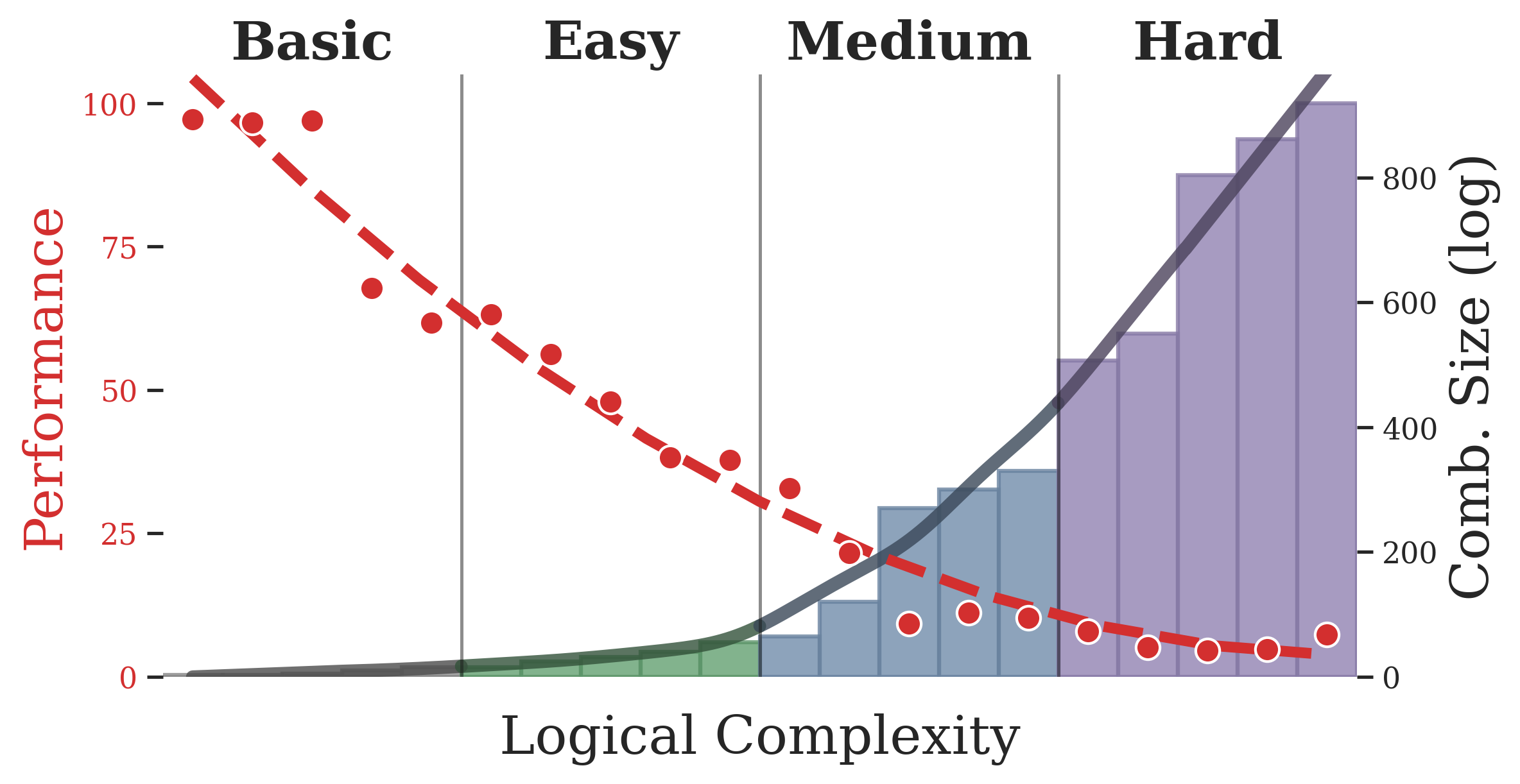
🧠 SLR-Bench-French: Scalable Logical Reasoning Benchmark (French Edition)
SLR-Bench Multilingual Versions:
SLR-Bench-French is the French-language pendant of the original SLR-Bench dataset. It follows the same symbolic structure, evaluation framework, and curriculum as the English version but provides all natural-language task prompts translated into French.
This enables systematic evaluation and training of Large Language Models (LLMs) in logical reasoning in French, supporting both multilingual reasoning and cross-lingual generalization research.
DS Overview
- Curriculum: 20 complexity levels, grouped into 4 broad tiers (basic, easy, medium, hard)
- Tasks: >19,000, each comprising: A natural language prompt, an executable validation program for automatic evaluation, and a latent ground-truth rule.
- Application: SLR-Bench can used to evaluate conventional and reasoning LLMs (e.g., GPT-4o, Llama-3, Gemini, DeepSeek-R1) and to train models via curriculum learning.
Key Features of SLR
- 🔨 Automatic Task Generation: Synthesize new inductive reasoning tasks with controllable complexity, novel logic rules, and natural language prompts—no need for human annotation.
- 🧩 Programmable & Scalable: Specify your own logic vocabulary, grammar, rule distributions, and task parameters; supports curriculum-style scaling and out-of-distribution task creation.
- 🧠 Symbolic, Automated Evaluation: Deterministically verify LLM outputs via the validation program, not MCQA, LLM judge, or exact matching.
- 📈 Curriculum Learning: Use SLR-Bench, a structured 20-level benchmark, for evaluating and training models across a span of logical challenges.
Quick Start
Loading the Dataset
from datasets import load_dataset
# Load SLR-Bench test split
ds = load_dataset("AIML-TUDA/SLR-Bench-French", "v1-All", split="test")
Evaluate using SLR-Bench
Requires the evaluate library and a Prolog interpreter installed on your system (e.g., SWI-Prolog).
Install the required dependencies via:
pip install evaluate
sudo apt-get install swi-prolog
Example Usage
from evaluate import load
symbolic_judge = load("AIML-TUDA/VerifiableRewardsForScalableLogicalReasoning")
rules = ds["ground-truth rule"] # For demo only—use model predictions in practice
references = [
{
"validation_program": p,
"evaluation_config": {
"positive_predicate": "est",
"negative_predicate": "ouest"
}
} for p in ds["validation program"]
]
results = symbolic_judge.compute(predictions=rules, references=references)
print(results)
Note: For real evaluation, replace rules with your model's predicted rules. Here, we use ground-truth rules for demonstration only.
Example results:
{'accuracy': 1.0,
'partial_score': 1.0,
'syntax_score': 1.0,
'detailed_results': [{'is_correct': True,'partial_score': 1.0,'syntax_valid': True,'error': None,'exec_time1': 0.014362812042236328},
{'is_correct': True,'partial_score': 1.0,'syntax_valid': True,'error': None,'exec_time1': 0.012364625930786133}]
}
Dataset Columns
| Column Name | Type | Description |
|---|---|---|
| id | int64 |
Unique identifier for each dataset entry (row). |
| prompt | string |
The instruction prompt of the logical reasoning task. |
| ground-truth rule | string |
The latent logical rule that solves the given task. |
| validation program | string |
The executable logic program used by the symbolic judge to verify candidate model solutions for the task. |
| symbols | string |
Symbolic representation of the bckground knowledge |
| curriculum level | int64 |
The specific level (1-20) in the SLR-Bench curriculum that this task belongs to, reflecting difficulty. |
| curriculum tier | string |
The broader difficulty tier grouping multiple levels (e.g., "basic", "easy", "medium", "hard"). |
| rule sampling | string |
The policy or method used to generate the ground-truth rule (e.g., "uniform", "llm-guided"). |
| rule complexity | string |
The length of the logic rule, counting the number of used predicates without the has_car predicate. |
| background sampling | string |
The policy used to sample background knowledge for the task (e.g., "mirror", "uniform"). |
| problem size | int64 |
Total number of labeled examples (positive + negative) provided in the task instance. |
| vocabulary predicates | int64 |
Number of unique predicate symbols available in the vocabulary for constructing rules and background knowledge. |
| vocabulary car constants | string |
List of car constant symbols (e.g., "car1", "car2", ...) available in the vocabulary for the task. |
SLR-Bench Curriculum
| Stage | Level | #Consts | #Preds | κ (Problem Size) | Bπ (Background) | Rlen (Rule len) | Rsample (Rule Sample) | Comb. Size |
|---|---|---|---|---|---|---|---|---|
| Basic | 1 | 1 | 5 | 2 | mirror | 1 | uniform | 10³ |
| 2 | 1 | 5 | 2 | mirror | 1-2 | uniform | 10³ | |
| 3 | 1 | 5 | 4 | mirror | 1-2 | uniform | 10⁵ | |
| 4 | 2 | 5 | 4 | mirror | 1-2 | uniform | 10¹⁰ | |
| 5 | 2 | 5 | 6 | mirror | 1-2 | uniform | 10¹⁶ | |
| Easy | 6 | 2 | 5 | 6 | uniform | 1-2 | uniform/llm | 10¹⁶ |
| 7 | 2 | 6 | 6 | uniform | 1-2 | uniform/llm | 10²⁴ | |
| 8 | 2-3 | 6 | 8 | uniform | 1-2 | uniform/llm | 10³² | |
| 9 | 2-3 | 6 | 10 | uniform | 2-3 | uniform/llm | 10⁴⁰ | |
| 10 | 2-3 | 7 | 12 | uniform | 2-3 | uniform/llm | 10⁵⁵ | |
| Medium | 11 | 2-4 | 7 | 14 | uniform | 2-3 | uniform/llm | 10⁶⁵ |
| 12 | 2-4 | 9 | 16 | uniform | 3-4 | uniform/llm | 10¹²⁰ | |
| 13 | 4-6 | 9 | 18 | uniform | 3-4 | uniform/llm | 10²⁷¹ | |
| 14 | 4-6 | 9 | 20 | uniform | 4-5 | uniform/llm | 10³⁰⁰ | |
| 15 | 4-6 | 9 | 22 | uniform | 4-5 | uniform/llm | 10³³⁰ | |
| Hard | 16 | 5-6 | 10 | 24 | uniform | 4-5 | uniform/llm | 10⁵⁰⁷ |
| 17 | 5-6 | 10 | 26 | uniform | 4-5 | uniform/llm | 10⁵⁴⁹ | |
| 18 | 5-6 | 12 | 28 | uniform | 4-5 | uniform/llm | 10⁸⁰⁵ | |
| 19 | 5-6 | 12 | 30 | uniform | 5 | uniform/llm | 10⁸⁶¹ | |
| 20 | 5-6 | 12 | 32 | uniform | 5 | uniform/llm | 10⁹¹⁹ |
SLR-Bench Curriculum: level-wise configurations, detailing language and task parameters for each difficulty stage. Language complexity is systematically increased by expanding the number of car constants and predicates. Task configuration grows via adapting problem size, background sampling, rule length, and rule sampling strategy. The final column reports the approximate combinatorial size of unique tasks available at each level.
Licensing Information
SLR-Bench is made available under the CC BY license.
Citation
If you use this dataset or framework, please cite:
@incollection{helff2025slrautomatedsynthesisscalable,
title={SLR: Automated Synthesis for Scalable Logical Reasoning},
author={Lukas Helff and Ahmad Omar and Felix Friedrich and Antonia Wüst and Hikaru Shindo and Rupert Mitchell and Tim Woydt and Patrick Schramowski and Wolfgang Stammer and Kristian Kersting},
year={2025},
booktitle ={Working Notes of the NeurIPS Workshop on Foundations of Reasoning in Language Models},
url={https://arxiv.org/abs/2506.15787},
}
- Downloads last month
- 38









