Dataset Viewer
problem
stringlengths 28
7.48k
| solution
stringlengths 0
18.5k
| answer
stringclasses 1
value | problem_type
stringclasses 8
values | question_type
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class | source_dataset
stringclasses 1
value | source_split
stringclasses 1
value | __index_level_0__
int64 1
111k
|
|---|---|---|---|---|---|---|---|---|---|
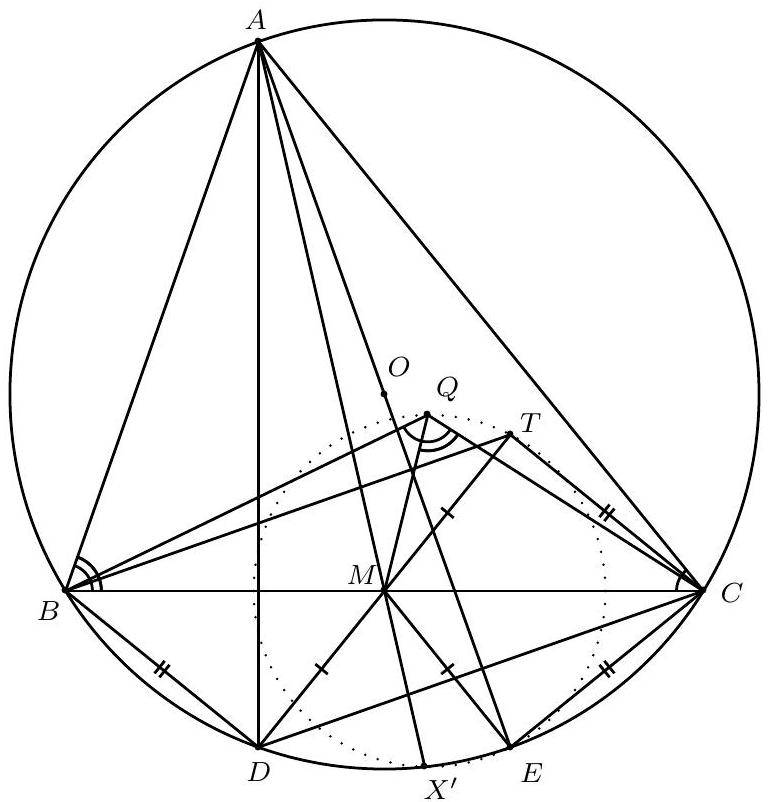
Problem 3. Triangle $A B C$ is such that $A B<A C$. The perpendicular bisector of side $B C$ intersects lines $A B$ and $A C$ at points $P$ and $Q$, respectively. Let $H$ be the orthocentre of triangle $A B C$, and let $M$ and $N$ be the midpoints of segments $B C$ and $P Q$, respectively. Prove that lines $H M$ and $A N$ meet on the circumcircle of $A B C$.
|
Solution. We have
$$
\angle A P Q=\angle B P M=90^{\circ}-\angle M B P=90^{\circ}-\angle C B A=\angle H C B
$$
and
$$
\angle A Q P=\angle M Q C=90^{\circ}-\angle Q C M=90^{\circ}-\angle A C B=\angle C B H
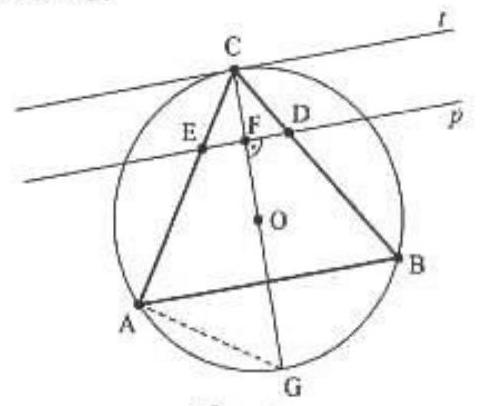
$$
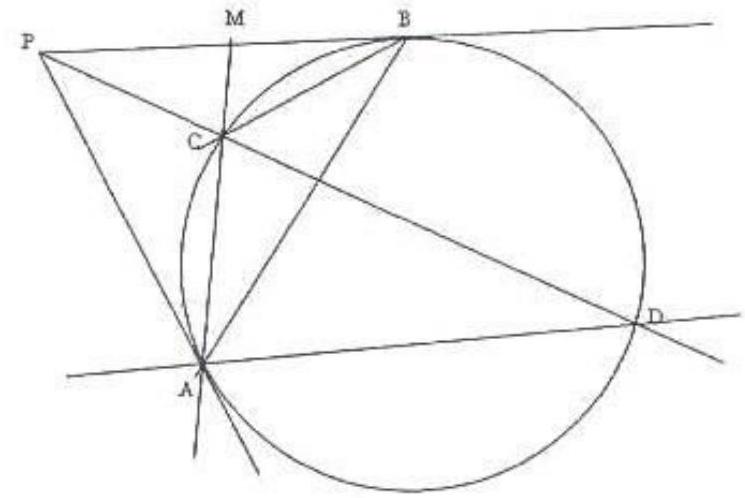
From these two equalities, we see that the triangles $A P Q$ and $H C B$ are similar. Moreover, since $M$ and $N$ are the midpoints of the segments $B C$ and $P Q$ respectively, then the triangles $A Q N$ and $H B M$ are also similar. Therefore, we have $\angle A N Q=\angle H M B$.
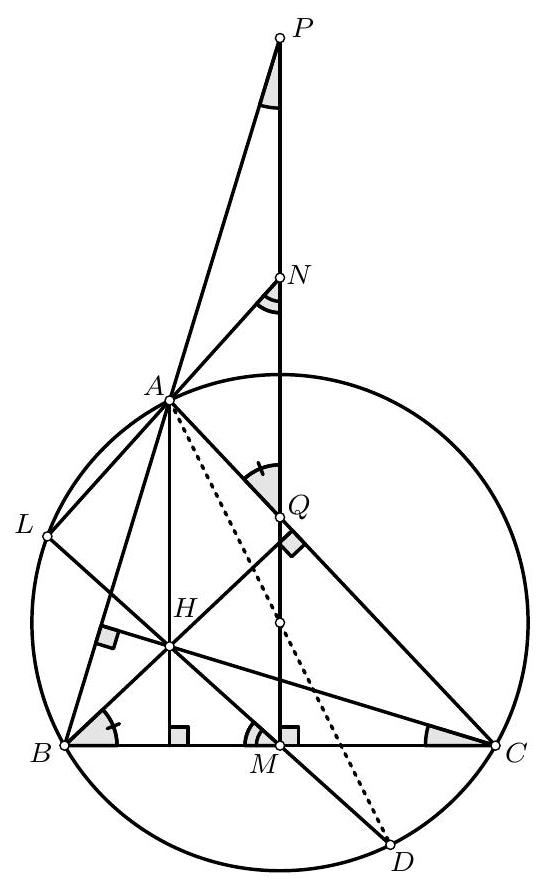
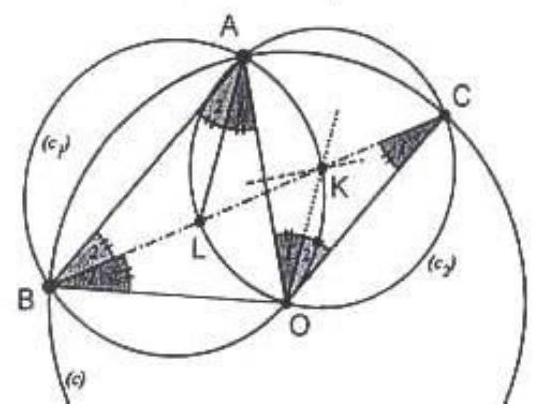
Let $L$ be the intersection of $A N$ and $H M$. We have
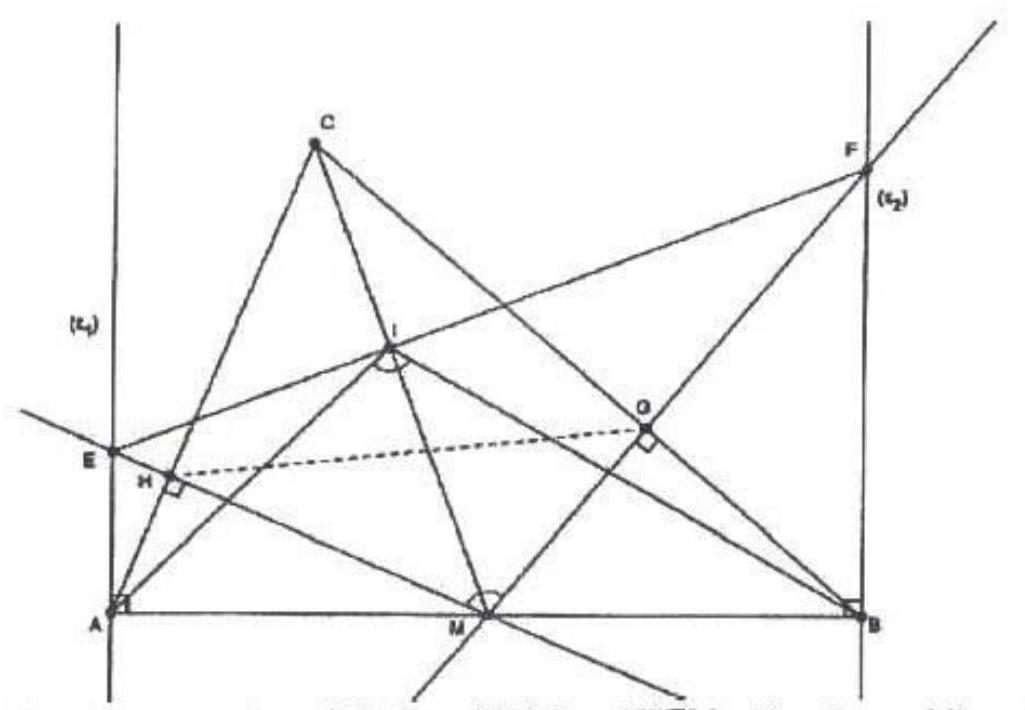
$$
\angle M L N=180^{\circ}-\angle L N M-\angle N M L=180^{\circ}-\angle L M B-\angle N M L=180^{\circ}-\angle N M B=90^{\circ} .
$$
Now let $D$ be the point on the circumcircle of $A B C$ diametrically oposite to $A$. It is known that $D$ is also the relfection of point $H$ over the point $M$. Therefore, we have that $D$ belongs on $M H$ and that $\angle D L A=\angle M L A=\angle M L N=90^{\circ}$. But, as $D A$ is the diameter of the circumcirle of $A B C$, the condition that $\angle D L A=90^{\circ}$ is enough to conclude that $L$ belongs on the circumcircle of $A B C$.
Remark. There is a spiral similarity mapping $A Q P$ to $H B C$. Since the similarity maps $A N$ to $H M$, it also maps $A H$ to $N M$, and since these two lines are parallel, the centre of the similarity is $L=A N \cap H M$. Since the similarity maps $B C$ to $Q P$, its centre belongs on the circumcircle of $B C X$, where $X=B Q \cap P C$. But $X$ is the reflection of $A$ on $Q M$ and so it must belong on the circumcircle of $A B C$. Hence so must $L$.
Remark. Students have also submitted correct proofs using radical axes, harmonic quadruples, coordinate geometry and complex numbers.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 1 |
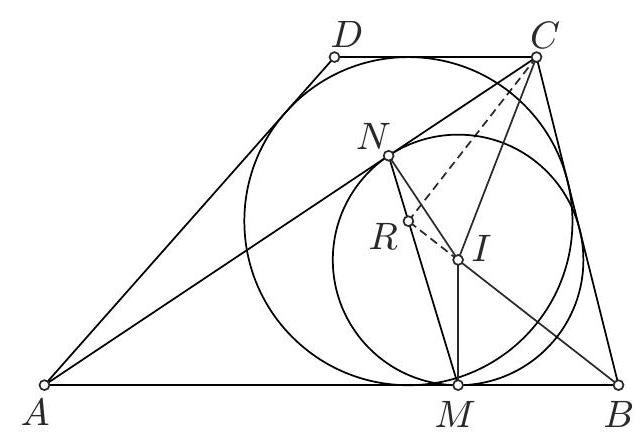
Problem 1. A trapezoid $A B C D(A B \| C D, A B>C D)$ is circumscribed. The incircle of the triangle $A B C$ touches the lines $A B$ and $A C$ at the points $M$ and $N$, respectively. Prove that the incenter of the trapezoid $A B C D$ lies on the line $M N$.
|
## Solution.
Version 1. Let $I$ be the incenter of triangle $A B C$ and $R$ be the common point of the lines $B I$ and $M N$. Since
$$
m(\widehat{A N M})=90^{\circ}-\frac{1}{2} m(\widehat{M A N}) \quad \text { and } \quad m(\widehat{B I C})=90^{\circ}+\frac{1}{2} m(\widehat{M A N})
$$
the quadrilateral $I R N C$ is cyclic.
It follows that $m(\widehat{B R C})=90^{\circ}$ and therefore
$$
m(\widehat{B C R})=90^{\circ}-m(\widehat{C B R})=90^{\circ}-\frac{1}{2}\left(180^{\circ}-m(\widehat{B C D})\right)=\frac{1}{2} m(\widehat{B C D})
$$
So, $(C R$ is the angle bisector of $\widehat{D C B}$ and $R$ is the incenter of the trapezoid.
Version 2. If $R$ is the incentre of the trapezoid $A B C D$, then $B, I$ and $R$ are collinear,
and $m(\widehat{B R C})=90^{\circ}$.
The quadrilateral $I R N C$ is cyclic.
Then $m(\widehat{M N C})=90^{\circ}+\frac{1}{2} \cdot m(\widehat{B A C})$
and $m(\widehat{R N C})=m(\widehat{B I C})=90^{\circ}+\frac{1}{2} \cdot m(\widehat{B A C})$,
so that $m(\widehat{M N C})=m(\widehat{R N C})$ and the points $M, R$ and $N$ are collinear.
Version 3. If $R$ is the incentre of the trapezoid $A B C D$, let $M^{\prime} \in(A B)$ and $N^{\prime} \in(A C)$ be the unique points, such that $R \in M^{\prime} N^{\prime}$ and $\left(A M^{\prime}\right) \equiv\left(A N^{\prime}\right)$.
Let $S$ be the intersection point of $C R$ and $A B$. Then $C R=R S$.
Consider $K \in A C$ such that $S K \| M^{\prime} N^{\prime}$. Then $N^{\prime}$ is the midpoint of $(C K)$.
We deduce
$$
A N^{\prime}=\frac{A K+A C}{2}=\frac{A S+A C}{2}=\frac{A B-B S+A C}{2}=\frac{A B+A C-B C}{2}=A N
$$
We conclude that $N=N^{\prime}$, hence $M=M^{\prime}$, and $R, M, N$ are collinear.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 2 |
Problem 2. Let $a, b$ and $c$ be positive real numbers. Prove that
$$
\frac{8}{(a+b)^{2}+4 a b c}+\frac{8}{(b+c)^{2}+4 a b c}+\frac{8}{(c+a)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \geq \frac{8}{a+3}+\frac{8}{b+3}+\frac{8}{c+3}
$$
|
Solution. Since $2 a b \leq a^{2}+b^{2}$, it follows that $(a+b)^{2} \leq 2\left(a^{2}+b^{2}\right)$
and $4 a b c \leq 2 c\left(a^{2}+b^{2}\right)$, for any positive reals $a, b, c$.
Adding these inequalities, we find
$$
(a+b)^{2}+4 a b c \leq 2\left(a^{2}+b^{2}\right)(c+1)
$$
so that
$$
\frac{8}{(a+b)^{2}+4 a b c} \geq \frac{4}{\left(a^{2}+b^{2}\right)(c+1)}
$$
Using the AM-GM inequality, we have
$$
\frac{4}{\left(a^{2}+b^{2}\right)(c+1)}+\frac{a^{2}+b^{2}}{2} \geq 2 \sqrt{\frac{2}{c+1}}=\frac{4}{\sqrt{2(c+1)}}
$$
respectively
$$
\frac{c+3}{8}=\frac{(c+1)+2}{8} \geq \frac{\sqrt{2(c+1)}}{4}
$$
We conclude that
$$
\frac{4}{\left(a^{2}+b^{2}\right)(c+1)}+\frac{a^{2}+b^{2}}{2} \geq \frac{8}{c+3}
$$
and finally
$$
\frac{8}{(a+b)^{2}+4 a b c}+\frac{8}{(a+c)^{2}+4 a b c}+\frac{8}{(b+c)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \geq \frac{8}{a+3}+\frac{8}{b+3}+\frac{8}{c+3}
$$
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 3 |
Problem 4. Let $A B C$ be an acute triangle, $A^{\prime}, B^{\prime}$ and $C^{\prime}$ be the reflections of the vertices $A, B$ and $C$ with respect to $B C, C A$, and $A B$, respectively, and let the circumcircles of triangles $A B B^{\prime}$ and $A C C^{\prime}$ meet again at $A_{1}$. Points $B_{1}$ and $C_{1}$ are defined similarly. Prove that the lines $A A_{1}, B B_{1}$ and $C C_{1}$ have a common point.
|
Solution. Let $O_{1}, O_{2}$ and $O$ be the circumcenters of triangles $A B B^{\prime}, A C C^{\prime}$ and $A B C$ respectively. As $A B$ is the perpendicular bisector of the line segment $C C^{\prime}, O_{2}$ is the intersection of the perpendicular bisector of $A C$ with $A B$. Similarly, $O_{1}$ is the intersection of the perpendicular bisector of $A B$ with $A C$. It follows that $O$ is the orthocenter of triangle $A O_{1} O_{2}$. This means that $A O$ is perpendicular to $O_{1} O_{2}$. On the other hand, the segment $A A_{1}$ is the common chord of the two circles, thus it is perpendicular to $O_{1} O_{2}$. As a result, $A A_{1}$ passes through $O$. Similarly, $B B_{1}$ and $C C_{1}$ pass through $O$, so the three lines are concurrent at $O$.
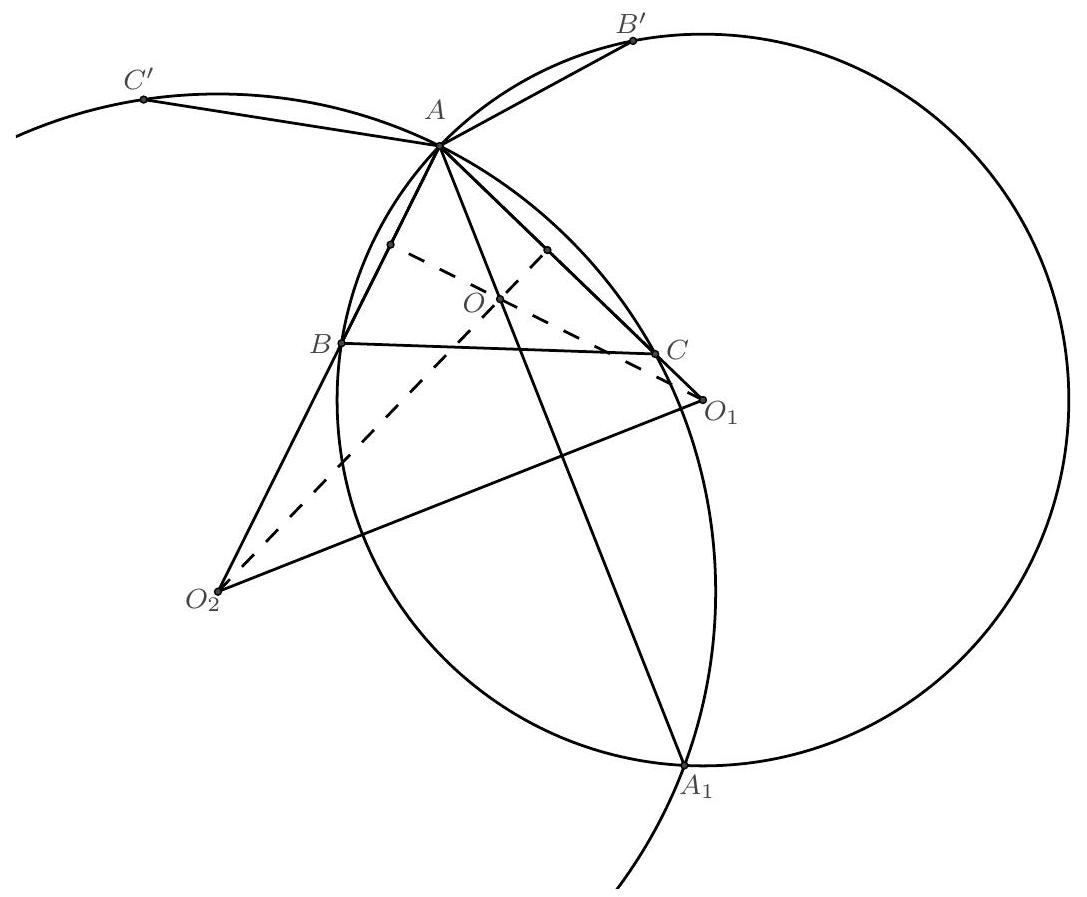
Comment by PSC. We present here a different approach.
We first prove that $A_{1}, B$ and $C^{\prime}$ are collinear. Indeed, since $\angle B A B^{\prime}=\angle C A C^{\prime}=2 \angle B A C$, then from the circles $\left(A B B^{\prime}\right),\left(A C C^{\prime}\right)$ we get
$$
\angle A A_{1} B=\frac{\angle B A_{1} B^{\prime}}{2}=\frac{180^{\circ}-\angle B A B^{\prime}}{2}=90^{\circ}-\angle B A C=\angle A A_{1} C^{\prime}
$$
It follows that
$$
\angle A_{1} A C=\angle A_{1} C^{\prime} C=\angle B C^{\prime} C=90^{\circ}-\angle A B C
$$
On the other hand, if $O$ is the circumcenter of $A B C$, then
$$
\angle O A C=90^{\circ}-\angle A B C \text {. }
$$
From (1) and (2) we conclude that $A_{1}, A$ and $O$ are collinear. Similarly, $B B_{1}$ and $C C_{1}$ pass through $O$, so the three lines are concurrent in $O$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 4 |
Problem 1. The real numbers $a, b, c, d$ satisfy simultaneously the equations
$$
a b c-d=1, b c d-a=2, c d a-b=3, d a b-c=-6
$$
Prove that $a+b+c+d \neq 0$.
|
Solution. Suppose that $a+b+c+d=0$. Then
$$
a b c+b c d+c d a+d a b=0
$$
If $a b c d=0$, then one of numbers, say $d$, must be 0 . In this case $a b c=0$, and so at least two of the numbers $a, b, c, d$ will be equal to 0 , making one of the given equations impossible. Hence $a b c d \neq 0$ and, from (1),
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}=0
$$
implying
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}
$$
It follows that $(a+b)(b+c)(c+a)=0$, which is impossible (for instance, if $a+b=0$, then adding the second and third given equations would lead to $0=2+3$, a contradiction). Thus $a+b+c+d \neq 0$.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 6 |
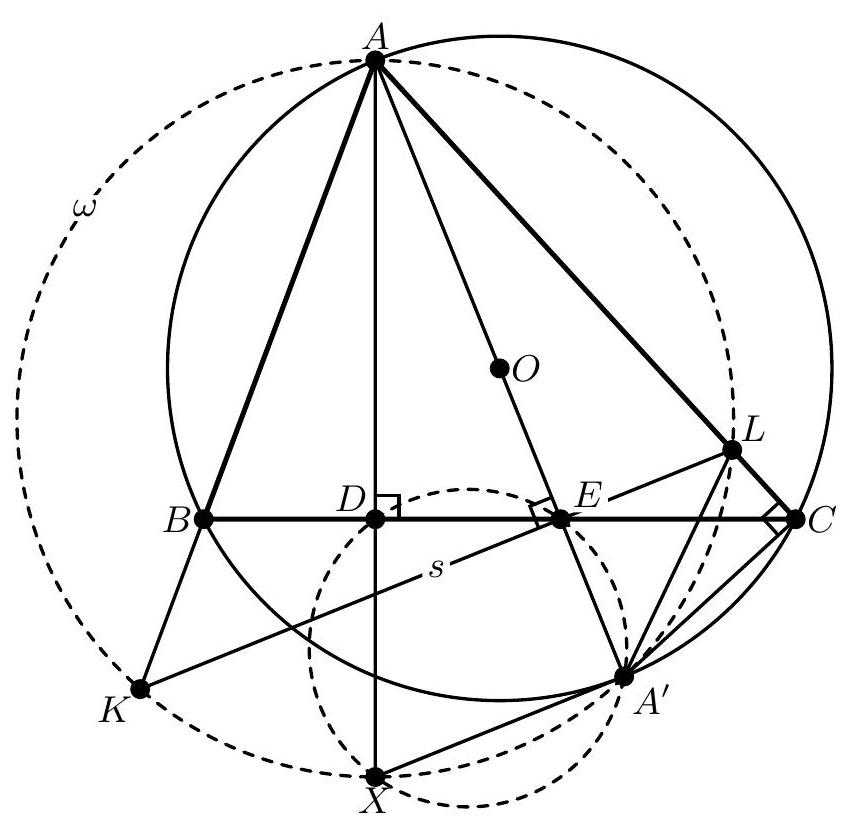
Problem 3. Let $A B C$ be an acute scalene triangle with circumcenter $O$. Let $D$ be the foot of the altitude from $A$ to the side $B C$. The lines $B C$ and $A O$ intersect at $E$. Let $s$ be the line through $E$ perpendicular to $A O$. The line $s$ intersects $A B$ and $A C$ at $K$ and $L$, respectively. Denote by $\omega$ the circumcircle of triangle $A K L$. Line $A D$ intersects $\omega$ again at $X$.
Prove that $\omega$ and the circumcircles of triangles $A B C$ and $D E X$ have a common point.
|
## Solution.
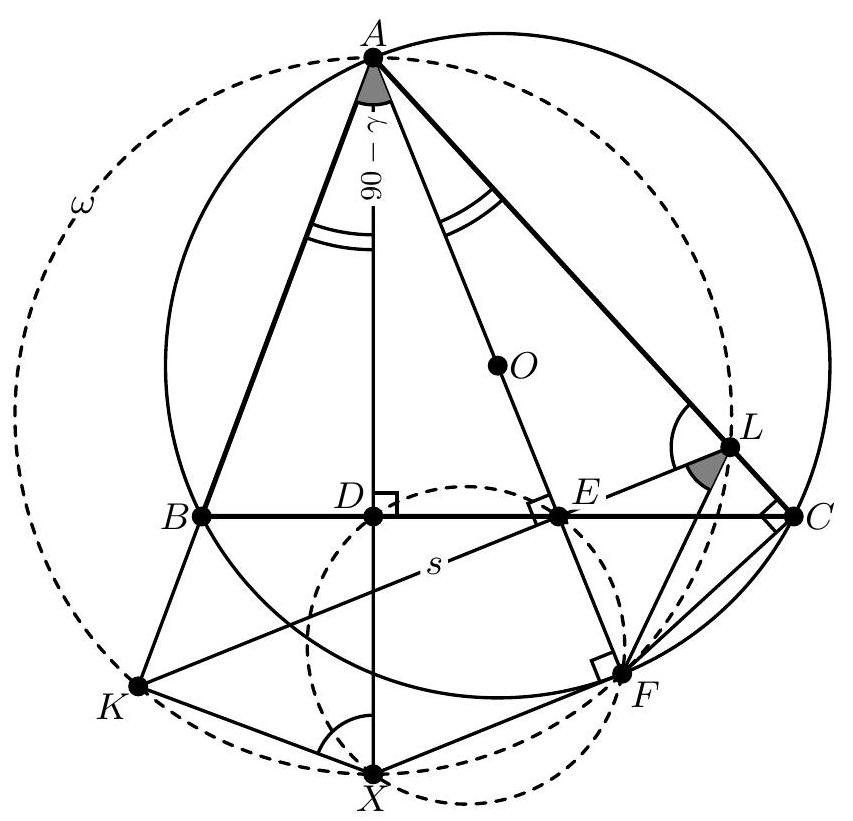
Let us denote angles of triangle $A B C$ with $\alpha, \beta, \gamma$ in a standard way. By basic anglechasing we have
$$
\angle B A D=90^{\circ}-\beta=\angle O A C \text { and } \angle C A D=\angle B A O=90^{\circ}-\gamma
$$
Using the fact that lines $A E$ and $A X$ are isogonal with respect to $\angle K A L$ we can conclude that $X$ is an $A$-antipode on $\omega$. (This fact can be purely angle-chased: we have
$$
\angle K A X+\angle A X K=\angle K A X+\angle A L K=90^{\circ}-\beta+\beta=90^{\circ}
$$
which implies $\angle A K X=90^{\circ}$ ). Now let $F$ be the projection of $X$ on the line $A E$. Using that $A X$ is a diameter of $\omega$ and $\angle E D X=90^{\circ}$ it's clear that $F$ is the intersection point of $\omega$ and the circumcircle of triangle $D E X$. Now it suffices to show that $A B F C$ is cyclic. We have $\angle K L F=\angle K A F=90^{\circ}-\gamma$ and from $\angle F E L=90^{\circ}$ we have that $\angle E F L=\gamma=\angle E C L$ so quadrilateral $E F C L$ is cyclic. Next, we have
$$
\angle A F C=\angle E F C=180^{\circ}-\angle E L C=\angle E L A=\beta
$$
(where last equality holds because of $\angle A E L=90^{\circ}$ and $\angle E A L=90^{\circ}-\beta$ ).
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 8 |
Problem 3. Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq 3(a+b+c+1)
$$
When does equality hold?
|
Solution 1. By using AM-GM $\left(x^{2}+y^{2}+z^{2} \geq x y+y z+z x\right)$ we have
$$
\begin{aligned}
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} & \geq\left(a+\frac{1}{b}\right)\left(b+\frac{1}{c}\right)+\left(b+\frac{1}{c}\right)\left(c+\frac{1}{a}\right)+\left(c+\frac{1}{a}\right)\left(a+\frac{1}{b}\right) \\
& =\left(a b+1+\frac{a}{c}+a\right)+\left(b c+1+\frac{b}{a}+b\right)+\left(c a+1+\frac{c}{b}+c\right) \\
& =a b+b c+c a+\frac{a}{c}+\frac{c}{b}+\frac{b}{a}+3+a+b+c
\end{aligned}
$$
Notice that by AM-GM we have $a b+\frac{b}{a} \geq 2 b, b c+\frac{c}{b} \geq 2 c$, and $c a+\frac{a}{c} \geq 2 a$.
Thus ,
$\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq\left(a b+\frac{b}{a}\right)+\left(b c+\frac{c}{b}\right)+\left(c a+\frac{a}{c}\right)+3+a+b+c \geq 3(a+b+c+1)$.
The equality holds if and only if $a=b=c=1$.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 9 |
Problem 2. Let $A B C$ be an acute triangle such that $A H=H D$, where $H$ is the orthocenter of $A B C$ and $D \in B C$ is the foot of the altitude from the vertex $A$. Let $\ell$ denote the line through $H$ which is tangent to the circumcircle of the triangle $B H C$. Let $S$ and $T$ be the intersection points of $\ell$ with $A B$ and $A C$, respectively. Denote the midpoints of $B H$ and $C H$ by $M$ and $N$, respectively. Prove that the lines $S M$ and $T N$ are parallel.
|
Solution 1. In order to prove that $S M$ and $T N$ are parallel, it suffices to prove that both of them are perpendicular to $S T$. Due to symmetry, we will provide a detailed proof of $S M \perp S T$, whereas the proof of $T N \perp S T$ is analogous. In this solution we will use the following notation: $\angle B A C=\alpha, \angle A B C=\beta, \angle A C B=\gamma$.
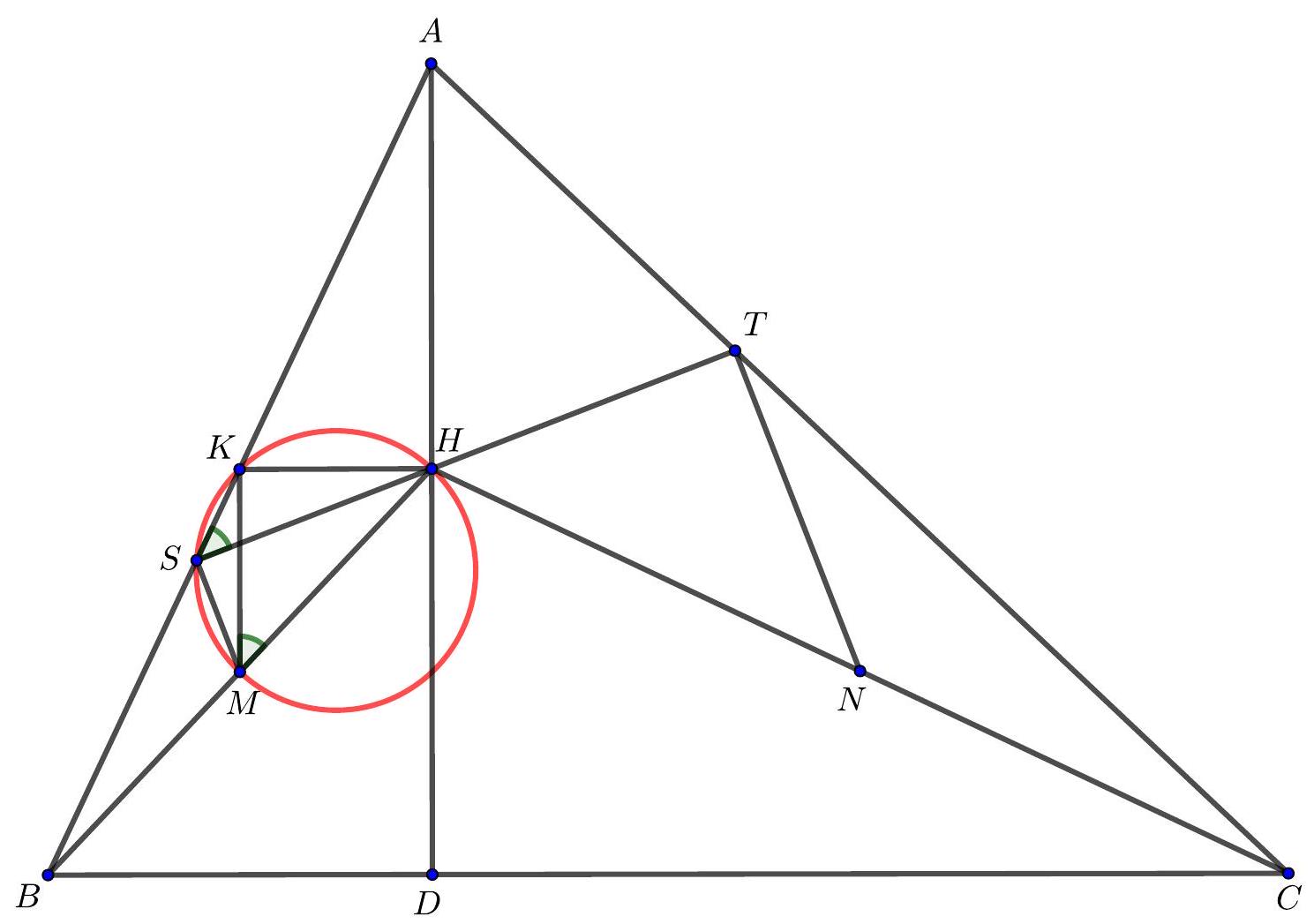
We first observe that, due to the tangency condition, we have
$$
\angle S H B=\angle H C B=90^{\circ}-\beta
$$
Combining the above with
$$
\angle S B H=\angle A B H=90^{\circ}-\alpha
$$
we get
$$
\angle B S H=180^{\circ}-\left(90^{\circ}-\beta\right)-\left(90^{\circ}-\alpha\right)=\alpha+\beta=180^{\circ}-\gamma
$$
from which it follows that $\angle A S T=\gamma$.
Since $A H=H D, H$ is the midpoint of $A D$. If $K$ denotes the midpoint of $A B$, we have that $K H$ and $B C$ are parallel. Since $M$ is the midpoint of $B H$, the lines $K M$ and $A D$ are parallel, from which it follows that $K M$ is perpendicular to $B C$. As $K H$ and $B C$ are parallel, we have that $K M$ is perpendicular to $K H$ so $\angle M K H=90^{\circ}$. Using the parallel lines $K H$ and $B C$ we also have
$$
\angle K H M=\angle K H B=\angle H B C
$$
Now,
$$
\angle H M K=90^{\circ}-\angle K H M=90^{\circ}-\angle H B C=90^{\circ}-\left(90^{\circ}-\gamma\right)=\gamma=\angle A S T=\angle K S H
$$
so the quadrilateral $M S K H$ is cyclic, which implies that $\angle M S H=\angle M K H=90^{\circ}$. In other words, the lines $S M$ and $S T$ are perpendicular, which completes our proof.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 10 |
## Problem 2.
Prove that for all non-negative real numbers $x, y, z$, not all equal to 0 , the following inequality holds
$$
\frac{2 x^{2}-x+y+z}{x+y^{2}+z^{2}}+\frac{2 y^{2}+x-y+z}{x^{2}+y+z^{2}}+\frac{2 z^{2}+x+y-z}{x^{2}+y^{2}+z} \geqslant 3
$$
Determine all the triples $(x, y, z)$ for which the equality holds.
|
Solution. Let us first write the expression $L$ on the left hand side in the following way
$$
\begin{aligned}
L & =\left(\frac{2 x^{2}-x+y+z}{x+y^{2}+z^{2}}+2\right)+\left(\frac{2 y^{2}+x-y+z}{x^{2}+y+z^{2}}+2\right)+\left(\frac{2 z^{2}+x+y-z}{x^{2}+y^{2}+z}+2\right)-6 \\
& =\left(2 x^{2}+2 y^{2}+2 z^{2}+x+y+z\right)\left(\frac{1}{x+y^{2}+z^{2}}+\frac{1}{x^{2}+y+z^{2}}+\frac{1}{x^{2}+y^{2}+z}\right)-6
\end{aligned}
$$
If we introduce the notation $A=x+y^{2}+z^{2}, B=x^{2}+y+z^{2}, C=x^{2}+y^{2}+z$, then the previous relation becomes
$$
L=(A+B+C)\left(\frac{1}{A}+\frac{1}{B}+\frac{1}{C}\right)-6
$$
Using the arithmetic-harmonic mean inequality or Cauchy-Schwartz inequality for positive real numbers $A, B, C$, we easily obtain
$$
(A+B+C)\left(\frac{1}{A}+\frac{1}{B}+\frac{1}{C}\right) \geqslant 9
$$
so it holds $L \geqslant 3$.
The equality occurs if and only if $A=B=C$, which is equivalent to the system of equations
$$
x^{2}-y^{2}=x-y, \quad y^{2}-z^{2}=y-z, \quad x^{2}-z^{2}=x-z
$$
It follows easily that the only solutions of this system are
$(x, y, z) \in\{(t, t, t) \mid t>0\} \cup\{(t, t, 1-t) \mid t \in[0,1]\} \cup\{(t, 1-t, t) \mid t \in[0,1]\} \cup\{(1-t, t, t) \mid t \in[0,1]\}$.
PSC Remark We feel the equality case needs more explanations in order to have a complete solution, our suggestion follows:
Clearly if $x, y, z$ are all equal and not 0 satisfy the condition. Now suppose that not all of them are equal it means we can't simultaneously have $x+y=y+z=z+x=1$ otherwise we would have all $x, y, z$ equal to $\frac{1}{2}$ which we already discussed. We can suppose now that $x=y$ and $y+z=z+x=1$ where we get $z=1-x$. So, all triples which satisfy the equality are $(x, y, z)=(a, a, a),(b, b, 1-b)$ and all permutations for any $a>0$ and $b \in[0,1]$
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 11 |
Problem 2. Let $\triangle A B C$ be a right-angled triangle with $\angle B A C=90^{\circ}$ and let $E$ be the foot of the perpendicular from $A$ on $B C$. Let $Z \neq A$ be a point on the line $A B$ with $A B=B Z$. Let (c) be the circumcircle of the triangle $\triangle A E Z$. Let $D$ be the second point of intersection of $(c)$ with $Z C$ and let $F$ be the antidiametric point of $D$ with respect to (c). Let $P$ be the point of intersection of the lines $F E$ and $C Z$. If the tangent to (c) at $Z$ meets $P A$ at $T$, prove that the points $T, E, B, Z$ are concyclic.
|
Solution. We will first show that $P A$ is tangent to $(c)$ at $A$.
Since $E, D, Z, A$ are concyclic, then $\angle E D C=\angle E A Z=\angle E A B$. Since also the triangles $\triangle A B C$ and $\triangle E B A$ are similar, then $\angle E A B=\angle B C A$, therefore $\angle E D C=\angle B C A$.
Since $\angle F E D=90^{\circ}$, then $\angle P E D=90^{\circ}$ and so
$$
\angle E P D=90^{\circ}-\angle E D C=90^{\circ}-\angle B C A=\angle E A C
$$
Therefore the points $E, A, C, P$ are concyclic. It follows that $\angle C P A=90^{\circ}$ and therefore the triangle $\angle P A Z$ is right-angled. Since also $B$ is the midpoint of $A Z$, then $P B=A B=B Z$ and so $\angle Z P B=$ $\angle P Z B$.
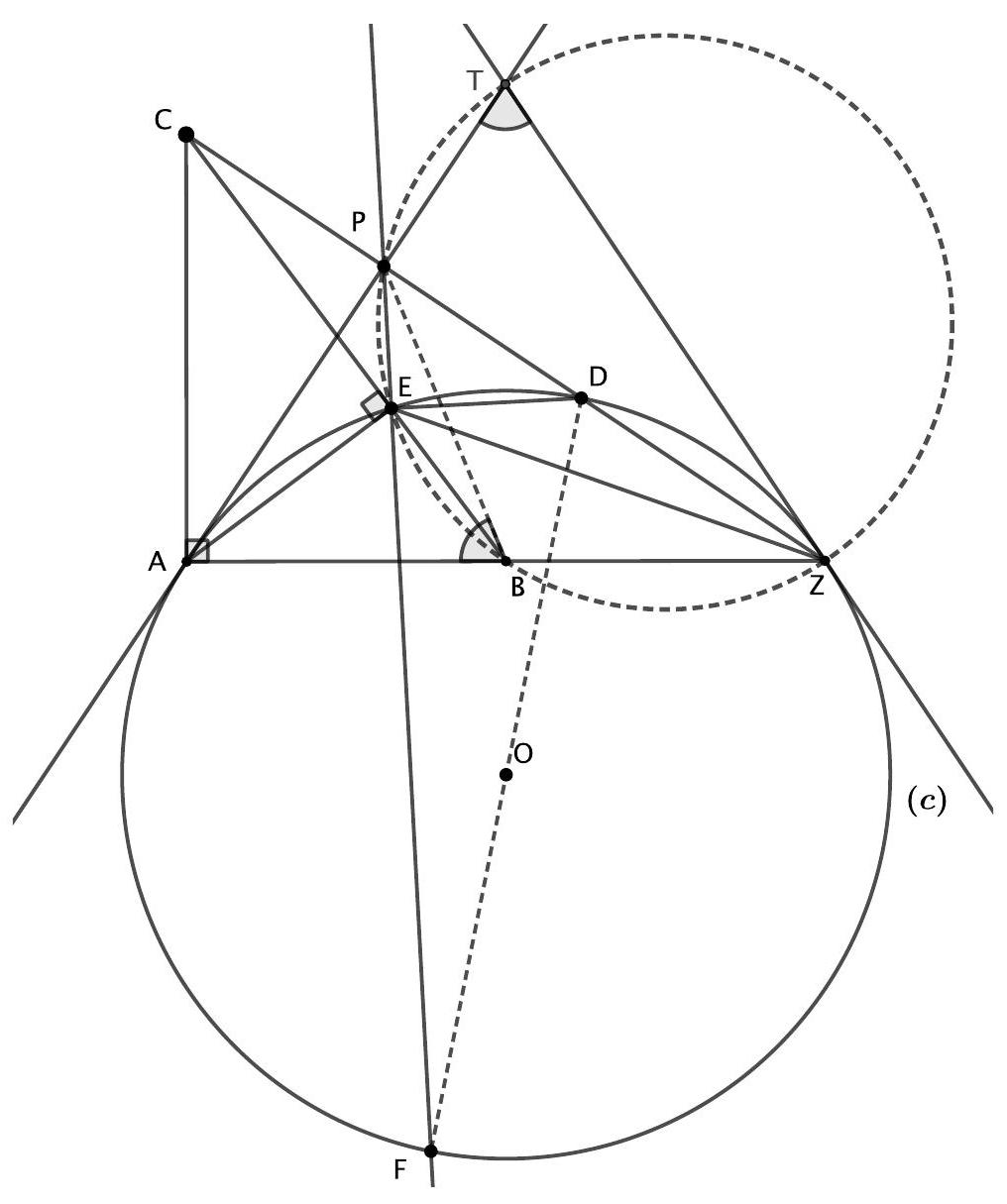
Furthermore, $\angle E P D=\angle E A C=\angle C B A=\angle E B A$ from which it follows that the points $P, E, B, Z$ are also concyclic.
Now observe that
$$
\angle P A E=\angle P C E=\angle Z P B-\angle P B E=\angle P Z B-\angle P Z E=\angle E Z B
$$
Therefore $P A$ is tangent to $(c)$ at $A$ as claimed.
It now follows that $T A=T Z$. Therefore
$$
\begin{aligned}
\angle P T Z & =180^{\circ}-2(\angle T A B)=180^{\circ}-2(\angle P A E+\angle E A B)=180^{\circ}-2(\angle E C P+\angle A C B) \\
& =180^{\circ}-2\left(90^{\circ}-\angle P Z B\right)=2(\angle P Z B)=\angle P Z B+\angle B P Z=\angle P B A .
\end{aligned}
$$
Thus $T, P, B, Z$ are concyclic, and since $P, E, B, Z$ are also concyclic then $T, E, B, Z$ are concyclic as required.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 13 |
Problem 2. Let $x, y, z$ be positive integers such that $x \neq y \neq z \neq x$. Prove that
$$
(x+y+z)(x y+y z+z x-2) \geq 9 x y z
$$
When does the equality hold?
|
Solution. Since $x, y, z$ are distinct positive integers, the required inequality is symmetric and WLOG we can suppose that $x \geq y+1 \geq z+2$. We consider 2 possible cases:
Case 1. $y \geq z+2$. Since $x \geq y+1 \geq z+3$ it follows that
$$
(x-y)^{2} \geq 1, \quad(y-z)^{2} \geq 4, \quad(x-z)^{2} \geq 9
$$
which are equivalent to
$$
x^{2}+y^{2} \geq 2 x y+1, \quad y^{2}+z^{2} \geq 2 y z+4, \quad x^{2}+z^{2} \geq 2 x z+9
$$
or otherwise
$$
z x^{2}+z y^{2} \geq 2 x y z+z, \quad x y^{2}+x z^{2} \geq 2 x y z+4 x, \quad y x^{2}+y z^{2} \geq 2 x y z+9 y
$$
Adding up the last three inequalities we have
$$
x y(x+y)+y z(y+z)+z x(z+x) \geq 6 x y z+4 x+9 y+z
$$
which implies that $(x+y+z)(x y+y z+z x-2) \geq 9 x y z+2 x+7 y-z$.
Since $x \geq z+3$ it follows that $2 x+7 y-z \geq 0$ and our inequality follows.
Case 2. $y=z+1$. Since $x \geq y+1=z+2$ it follows that $x \geq z+2$, and replacing $y=z+1$ in the required inequality we have to prove
$$
(x+z+1+z)(x(z+1)+(z+1) z+z x-2) \geq 9 x(z+1) z
$$
which is equivalent to
$$
(x+2 z+1)\left(z^{2}+2 z x+z+x-2\right)-9 x(z+1) z \geq 0
$$
Doing easy algebraic manipulations, this is equivalent to prove
$$
(x-z-2)(x-z+1)(2 z+1) \geq 0
$$
which is satisfied since $x \geq z+2$.
The equality is achieved only in the Case 2 for $x=z+2$, so we have equality when $(x, y, z)=$ $(k+2, k+1, k)$ and all the permutations for any positive integer $k$.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 14 |
Problem 3. Let $A B C$ be an acute triangle such that $A B \neq A C$, with circumcircle $\Gamma$ and circumcenter $O$. Let $M$ be the midpoint of $B C$ and $D$ be a point on $\Gamma$ such that $A D \perp B C$. Let $T$ be a point such that $B D C T$ is a parallelogram and $Q$ a point on the same side of $B C$ as $A$ such that
$$
\angle B Q M=\angle B C A \quad \text { and } \quad \angle C Q M=\angle C B A
$$
Let the line $A O$ intersect $\Gamma$ at $E,(E \neq A)$ and let the circumcircle of $\triangle E T Q$ intersect $\Gamma$ at point $X \neq E$. Prove that the points $A, M$, and $X$ are collinear.
|
Solution. Let $X^{\prime}$ be symmetric point to $Q$ in line $B C$. Now since $\angle C B A=\angle C Q M=\angle C X^{\prime} M$, $\angle B C A=\angle B Q M=\angle B X^{\prime} M$, we have
$$
\angle B X^{\prime} C=\angle B X^{\prime} M+\angle C X^{\prime} M=\angle C B A+\angle B C A=180^{\circ}-\angle B A C
$$
we have that $X^{\prime} \in \Gamma$. Now since $\angle A X^{\prime} B=\angle A C B=\angle M X^{\prime} B$ we have that $A, M, X^{\prime}$ are collinear. Note that since
$$
\angle D C B=\angle D A B=90^{\circ}-\angle A B C=\angle O A C=\angle E A C
$$
we get that $D B C E$ is an isosceles trapezoid.
Since $B D C T$ is a parallelogram we have $M T=M D$, with $M, D, T$ being collinear, $B D=C T$, and since $B D E C$ is an isosceles trapezoid we have $B D=C E$ and $M E=M D$. Since
$$
\angle B T C=\angle B D C=\angle B E D, \quad C E=B D=C T \quad \text { and } \quad M E=M T
$$
we have that $E$ and $T$ are symmetric with respect to the line $B C$. Now since $Q$ and $X^{\prime}$ are symmetric with respect to the line $B C$ as well, this means that $Q X^{\prime} E T$ is an isosceles trapezoid which means that $Q, X^{\prime}, E, T$ are concyclic. Since $X^{\prime} \in \Gamma$ this means that $X \equiv X^{\prime}$ and therefore $A, M, X$ are collinear.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 15 |
Problem 3. Let $\triangle A B C$ be an acute triangle. The lines $l_{1}, l_{2}$ are perpendicular to $A B$ at the points $A, B$ respectively. The perpendicular lines from the midpoint $M$ of $A B$ to the sides of the triangle $A C, B C$ intersect the lines $l_{1}, l_{2}$ at the points $E, F$, respectively. If $D$ is the intersection point of $E F$ and $M C$, prove that
$$
\angle A D B=\angle E M F
$$
|
## Solution:
Let $H, G$ be the points of intersection of $M E, M F$ with $A C, B C$ respectively. From the similarity of triangles $\triangle M H A$ and $\triangle M A E$ we get $\frac{M H}{M A}=\frac{M A}{M E}$, thus
$$
M A^{2}=M H \cdot M E
$$
Similarly, from the similarity of triangles $\triangle M B G$ and $\triangle M F B$ we get $\frac{M B}{M F}=\frac{M G}{M B}$, thus
$$
M B^{2}=M F \cdot M G
$$
Since $M A=M B$, from (1), (2), we conclude that the points $E, H, G, F$ are concyclic.
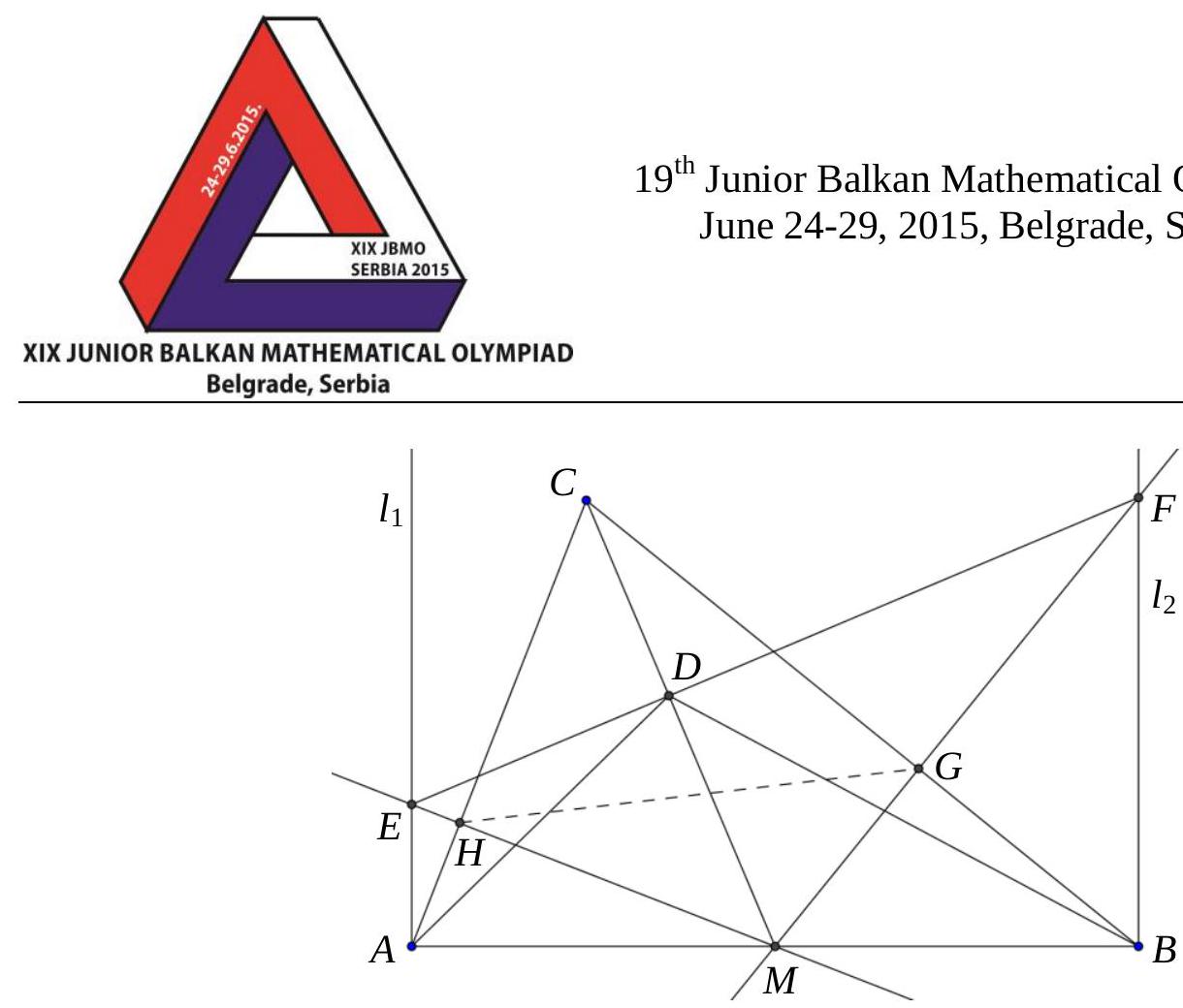
Therefore, we get that $\angle F E H=\angle F E M=\angle H G M$. Also, the quadrilateral $C H M G$ is cyclic, so $\angle C M H=\angle H G C$. We have
$$
\angle F E H+\angle C M H=\angle H G M+\angle H G C=90^{\circ}
$$
thus $C M \perp E F$. Now, from the cyclic quadrilaterals $F D M B$ and $E A M D$, we get that $\angle D F M=\angle D B M$ and $\angle D E M=\angle D A M$. Therefore, the triangles $\triangle E M F$ and $\triangle A D B$ are similar, so $\angle A D B=\angle E M F$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 16 |
A1. Let $a, b, c$ be positive real numbers such that $a+b+c+a b+b c+c a+a b c=7$. Prove that
$$
\sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} \geq 6
$$
|
Solution. First we see that $x^{2}+y^{2}+1 \geq x y+x+y$. Indeed, this is equivalent to
$$
(x-y)^{2}+(x-1)^{2}+(y-1)^{2} \geq 0
$$
Therefore
$$
\begin{aligned}
& \sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} \\
\geq & \sqrt{a b+a+b+1}+\sqrt{b c+b+c+1}+\sqrt{c a+c+a+1} \\
= & \sqrt{(a+1)(b+1)}+\sqrt{(b+1)(a+1)}+\sqrt{(c+1)(a+1)}
\end{aligned}
$$
It follows from the AM-GM inequality that
$$
\begin{aligned}
& \sqrt{(a+1)(b+1)}+\sqrt{(b+1)(a+1)}+\sqrt{(c+1)(a+1)} \\
\geq & 3 \sqrt[3]{\sqrt{(a+1)(b+1)} \cdot \sqrt{(b+1)(a+1)} \cdot \sqrt{(c+1)(a+1)}} \\
= & 3 \sqrt[3]{(a+1)(b+1)(c+1)}
\end{aligned}
$$
On the other hand, the given condition is equivalent to $(a+1)(b+1)(c+1)=8$ and we get the desired inequality.
Obviously, equality is attained if and only if $a=b=c=1$.
Remark. The condition of positivity of $a, b, c$ is superfluous and the equality $\cdots=7$ can be replaced by the inequality $\cdots \geq 7$. Indeed, the above proof and the triangle inequality imply that
$$
\begin{aligned}
\sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} & \geq 3 \sqrt[3]{(|a|+1)(|b|+1)(|c|+1)} \\
& \geq 3 \sqrt[3]{|a+1| \cdot|b+1| \cdot|c+1|} \geq 6
\end{aligned}
$$
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 17 |
A3. Let $a, b, c, d$ be real numbers such that $0 \leq a \leq b \leq c \leq d$. Prove the inequality
$$
a b^{3}+b c^{3}+c d^{3}+d a^{3} \geq a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}
$$
|
Solution. The inequality is equivalent to
$$
\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)^{2} \geq\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\right)^{2}
$$
By the Cauchy-Schwarz inequality,
$$
\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\right) \geq\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\right)^{2}
$$
Hence it is sufficient to prove that
$$
\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)^{2} \geq\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\right)
$$
i.e. to prove $a b^{3}+b c^{3}+c d^{3}+d a^{3} \geq a^{3} b+b^{3} c+c^{3} d+d^{3} a$.
This inequality can be written successively
$$
a\left(b^{3}-d^{3}\right)+b\left(c^{3}-a^{3}\right)+c\left(d^{3}-b^{3}\right)+d\left(a^{3}-c^{3}\right) \geq 0
$$
or
$$
(a-c)\left(b^{3}-d^{3}\right)-(b-d)\left(a^{3}-c^{3}\right) \geq 0
$$
which comes down to
$$
(a-c)(b-d)\left(b^{2}+b d+d^{2}-a^{2}-a c-c^{2}\right) \geq 0
$$
The last inequality is true because $a-c \leq 0, b-d \leq 0$, and $\left(b^{2}-a^{2}\right)+(b d-a c)+\left(d^{2}-c^{2}\right) \geq 0$ as a sum of three non-negative numbers.
The last inequality is satisfied with equality whence $a=b$ and $c=d$. Combining this with the equality cases in the Cauchy-Schwarz inequality we obtain the equality cases for the initial inequality: $a=b=c=d$.
Remark. Instead of using the Cauchy-Schwarz inequality, once the inequality $a b^{3}+b c^{3}+c d^{3}+$ $d a^{3} \geq a^{3} b+b^{3} c+c^{3} d+d^{3} a$ is established, we have $2\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right) \geq\left(a b^{3}+b c^{3}+c d^{3}+\right.$ $\left.d a^{3}\right)+\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\right)=\left(a b^{3}+a^{3} b\right)+\left(b c^{3}+b^{3} c\right)+\left(c d^{3}+c^{3} d\right)+\left(d a^{3}+d^{3} a\right) \stackrel{A M-G M}{\geq}$ $2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} d^{2}+2 d^{2} a^{2}$ which gives the conclusion.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 18 |
A4. Let $x, y, z$ be three distinct positive integers. Prove that
$$
(x+y+z)(x y+y z+z x-2) \geq 9 x y z
$$
When does the equality hold?
|
Solution. Since $x, y, z$ are distinct positive integers, the required inequality is symmetric and WLOG we can suppose that $x \geq y+1 \geq z+2$. We consider 2 possible cases:
Case 1. $y \geq z+2$. Since $x \geq y+1 \geq z+3$ it follows that
$$
(x-y)^{2} \geq 1, \quad(y-z)^{2} \geq 4, \quad(x-z)^{2} \geq 9
$$
which are equivalent to
$$
x^{2}+y^{2} \geq 2 x y+1, \quad y^{2}+z^{2} \geq 2 y z+4, \quad x^{2}+z^{2} \geq 2 x z+9
$$
or otherwise
$$
z x^{2}+z y^{2} \geq 2 x y z+z, \quad x y^{2}+x z^{2} \geq 2 x y z+4 x, \quad y x^{2}+y z^{2} \geq 2 x y z+9 y
$$
Adding up the last three inequalities we have
$$
x y(x+y)+y z(y+z)+z x(z+x) \geq 6 x y z+4 x+9 y+z
$$
which implies that $(x+y+z)(x y+y z+z x-2) \geq 9 x y z+2 x+7 y-z$.
Since $x \geq z+3$ it follows that $2 x+7 y-z \geq 0$ and our inequality follows.
Case 2. $y=z+1$. Since $x \geq y+1=z+2$ it follows that $x \geq z+2$, and replacing $y=z+1$ in the required inequality we have to prove
$$
(x+z+1+z)(x(z+1)+(z+1) z+z x-2) \geq 9 x(z+1) z
$$
which is equivalent to
$$
(x+2 z+1)\left(z^{2}+2 z x+z+x-2\right)-9 x(z+1) z \geq 0
$$
Doing easy algebraic manipulations, this is equivalent to prove
$$
(x-z-2)(x-z+1)(2 z+1) \geq 0
$$
which is satisfied since $x \geq z+2$.
The equality is achieved only in the Case 2 for $x=z+2$, so we have equality when $(x, y, z)=$ $(k+2, k+1, k)$ and all the permutations for any positive integer $k$.
## Combinatorics
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 19 |
G1. Given a parallelogram $A B C D$. The line perpendicular to $A C$ passing through $C$ and the line perpendicular to $B D$ passing through $A$ intersect at point $P$. The circle centered at point $P$ and radius $P C$ intersects the line $B C$ at point $X,(X \neq C)$ and the line $D C$ at point $Y$, $(Y \neq C)$. Prove that the line $A X$ passes through the point $Y$.
|
Solution. Denote the feet of the perpendiculars from $P$ to the lines $B C$ and $D C$ by $M$ and $N$ respectively and let $O=A C \cap B D$. Since the points $O, M$ and $N$ are midpoints of $C A, C X$ and $C Y$ respectively it suffices to prove that $M, N$ and $O$ are collinear. According to Menelaus's theorem for $\triangle B C D$ and points $M, N$ and $O$ we have to prove that
$$
\frac{B M}{M C} \cdot \frac{C N}{N D} \cdot \frac{D O}{O B}=1
$$
Since $D O=O B$ the above simplifies to $\frac{B M}{C M}=\frac{D N}{C N}$. It follows from $B M=B C+C M$ and $D N=D C-C N=A B-C N$ that the last equality is equivalent to:
$$
\frac{B C}{C M}+2=\frac{A B}{C N}
$$
Denote by $S$ the foot of the perpendicular from $B$ to $A C$. Since $\Varangle B C S=\Varangle C P M=\varphi$ and $\Varangle B A C=\Varangle A C D=\Varangle C P N=\psi$ we conclude that $\triangle C B S \sim \triangle P C M$ and $\triangle A B S \sim \triangle P C N$. Therefore
$$
\frac{C M}{B S}=\frac{C P}{B C} \text { and } \frac{C N}{B S}=\frac{C P}{A B}
$$
and thus,
$$
C M=\frac{C P . B S}{B C} \text { and } C N=\frac{C P . B S}{A B}
$$
Now equality (1) becomes $A B^{2}-B C^{2}=2 C P . B S$. It follows from
$$
A B^{2}-B C^{2}=A S^{2}-C S^{2}=(A S-C S)(A S+C S)=2 O S . A C
$$
that
$$
D C^{2}-B C^{2}=2 C P \cdot B S \Longleftrightarrow 2 O S \cdot A C=2 C P . B S \Longleftrightarrow O S \cdot A C=C P \cdot B S .
$$
Since $\Varangle A C P=\Varangle B S O=90^{\circ}$ and $\Varangle C A P=\Varangle S B O$ we conclude that $\triangle A C P \sim \triangle B S O$. This implies $O S . A C=C P . B S$, which completes the proof.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 20 |
G2. Let $A B C$ be an acute triangle such that $A B$ is the shortest side of the triangle. Let $D$ be the midpoint of the side $A B$ and $P$ be an interior point of the triangle such that
$$
\Varangle C A P=\Varangle C B P=\Varangle A C B
$$
Denote by $M$ and $N$ the feet of the perpendiculars from $P$ to $B C$ and $A C$, respectively. Let $p$ be the line through $M$ parallel to $A C$ and $q$ be the line through $N$ parallel to $B C$. If $p$ and $q$ intersect at $K$ prove that $D$ is the circumcenter of triangle $M N K$.
|
Solution. If $\gamma=\Varangle A C B$ then $\Varangle C A P=\Varangle C B P=\Varangle A C B=\gamma$. Let $E=K N \cap A P$ and $F=K M \cap B P$. We show that points $E$ and $F$ are midpoints of $A P$ and $B P$, respectively.
Indeed, consider the triangle $A E N$. Since $K N \| B C$, we have $\Varangle E N A=\Varangle B C A=\gamma$. Moreover $\Varangle E A N=\gamma$ giving that triangle $A E N$ is isosceles, i.e. $A E=E N$. Next, consider the triangle $E N P$. Since $\Varangle E N A=\gamma$ we find that
$$
\Varangle P N E=90^{\circ}-\Varangle E N A=90^{\circ}-\gamma
$$
Now $\Varangle E P N=90^{\circ}-\gamma$ implies that the triangle $E N P$ is isosceles triangle, i.e. $E N=E P$.
Since $A E=E N=E P$ point $E$ is the midpoint of $A P$ and analogously, $F$ is the midpoint of $B P$. Moreover, $D$ is also midpoint of $A B$ and we conclude that $D F P E$ is parallelogram.
It follows from $D E \| A P$ and $K E \| B C$ that $\Varangle D E K=\Varangle C B P=\gamma$ and analogously $\Varangle D F K=\gamma$.
We conclude that $\triangle E D N \cong \triangle F M D(E D=F P=F M, E N=E P=F D$ and $\Varangle D E N=$ $\left.\Varangle M F D=180^{\circ}-\gamma\right)$ and thus $N D=M D$. Therefore $D$ is a point on the perpendicular bisector of $M N$. Further,
$$
\begin{aligned}
\Varangle F D E & =\Varangle F P E=360^{\circ}-\Varangle B P M-\Varangle M P N-\Varangle N P A= \\
& =360^{\circ}-\left(90^{\circ}-\gamma\right)-\left(180^{\circ}-\gamma\right)-\left(90^{\circ}-\gamma\right)=3 \gamma
\end{aligned}
$$
It follows that
$$
\begin{aligned}
\Varangle M D N & =\Varangle F D E-\Varangle F D M-\Varangle E D N=\Varangle F D E-\Varangle E N D-\Varangle E D N= \\
& =\Varangle F D E-(\Varangle E N D+\Varangle E D N)=3 \gamma-\gamma=2 \gamma .
\end{aligned}
$$
Fianlly, $K M C N$ is parallelogram, i.e. $\Varangle M K N=\Varangle M C N=\gamma$. Therefore $D$ is a point on the perpendicular bisector of $M N$ and $\Varangle M D N=2 \Varangle M K N$, so $D$ is the circumcenter of $\triangle M N K$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 21 |
Problem G4. Let $A B C$ be a scalene triangle with circumcircle $\Gamma$ and circumcenter $O$. Let $M$ be the midpoint of $B C$ and $D$ be a point on $\Gamma$ such that $A D \perp B C$. Let $T$ be a point such that $B D C T$ is a parallelogram and $Q$ a point on the same side of $B C$ as $A$ such that
$$
\Varangle B Q M=\Varangle B C A \quad \text { and } \quad \Varangle C Q M=\Varangle C B A
$$
Let $A O$ intersect $\Gamma$ again at $E$ and let the circumcircle of $E T Q$ intersect $\Gamma$ at point $X \neq E$. Prove that the points $A, M$, and $X$ are collinear.
|
Solution. Let $X^{\prime}$ be symmetric point to $Q$ in line $B C$. Now since $\Varangle C B A=\Varangle C Q M=$ $\Varangle C X^{\prime} M, \Varangle B C A=\Varangle B Q M=\Varangle B X^{\prime} M$, we have
$$
\Varangle B X^{\prime} C=\Varangle B X^{\prime} M+\Varangle C X^{\prime} M=\Varangle C B A+\Varangle B C A=180^{\circ}-\Varangle B A C
$$
we have that $X^{\prime} \in \Gamma$. Now since $\Varangle A X^{\prime} B=\Varangle A C B=\Varangle M X^{\prime} B$ we have that $A, M, X^{\prime}$ are collinear. Note that since
$$
\Varangle D C B=\Varangle D A B=90^{\circ}-\Varangle A B C=\Varangle O A C=\Varangle E A C
$$
we get that $D B C E$ is an isosceles trapezoid.
Since $B D C T$ is a parallelogram we have $M T=M D$, with $M, D, T$ being collinear, $B D=C T$, and since $B D E C$ is an isosceles trapezoid we have $B D=C E$ and $M E=M D$. Since
$$
\Varangle B T C=\Varangle B D C=\Varangle B E D, \quad C E=B D=C T \quad \text { and } \quad M E=M T
$$
we have that $E$ and $T$ are symmetric with respect to the line $B C$. Now since $Q$ and $X^{\prime}$ are symmetric with respect to the line $B C$ as well, this means that $Q X^{\prime} E T$ is an isosceles trapezoid which means that $Q, X^{\prime}, E, T$ are concyclic. Since $X^{\prime} \in \Gamma$ this means that $X \equiv X^{\prime}$ and therefore $A, M, X$ are collinear.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 23 |
Problem G5. A point $P$ lies in the interior of the triangle $A B C$. The lines $A P, B P$, and $C P$ intersect $B C, C A$, and $A B$ at points $D, E$, and $F$, respectively. Prove that if two of the quadrilaterals $A B D E, B C E F, C A F D, A E P F, B F P D$, and $C D P E$ are concyclic, then all six are concyclic.
|
Solution. We first prove the following lemma:
Lemma 1. Let $A B C D$ be a convex quadrilateral and let $A B \cap C D=E$ and $B C \cap D A=F$. Then the circumcircles of triangles $A B F, C D F, B C E$ and $D A E$ all pass through a common point $P$. This point lies on line $E F$ if and only if $A B C D$ in concyclic.
Proof. Let the circumcircles of $A B F$ and $B C F$ intersect at $P \neq B$. We have
$$
\begin{aligned}
\Varangle F P C & =\Varangle F P B+\Varangle B P C=\Varangle B A D+\Varangle B E C=\Varangle E A D+\Varangle A E D= \\
& =180^{\circ}-\Varangle A D E=180^{\circ}-\Varangle F D C
\end{aligned}
$$
which gives us $F, P, C$ and $D$ are concyclic. Similarly we have
$$
\begin{aligned}
\Varangle A P E & =\Varangle A P B+\Varangle B P E=\Varangle A F B+\Varangle B C D=\Varangle D F C+\Varangle F C D= \\
& =180^{\circ}-\Varangle F D C=180^{\circ}-\Varangle A D E
\end{aligned}
$$
which gives us $E, P, A$ and $D$ are concyclic. Since $\Varangle F P E=\Varangle F P B+\Varangle E P B=\Varangle B A D+$ $\Varangle B C D$ we get that $\Varangle F P E=180^{\circ}$ if and only if $\Varangle B A D+\Varangle B C D=180^{\circ}$ which completes the lemma. We now divide the problem into cases:
Case 1: $A E P F$ and $B F E C$ are concyclic. Here we get that
$$
180^{\circ}=\Varangle A E P+\Varangle A F P=360^{\circ}-\Varangle C E B-\Varangle B F C=360^{\circ}-2 \Varangle C E B
$$
and here we get that $\Varangle C E B=\Varangle C F B=90^{\circ}$, from here it follows that $P$ is the ortocenter of $\triangle A B C$ and that gives us $\Varangle A D B=\Varangle A D C=90^{\circ}$. Now the quadrilaterals $C E P D$ and $B D P F$ are concyclic because
$$
\Varangle C E P=\Varangle C D P=\Varangle P D B=\Varangle P F B=90^{\circ} .
$$
Quadrilaterals $A C D F$ and $A B D E$ are concyclic because
$$
\Varangle A E B=\Varangle A D B=\Varangle A D C=\Varangle A F C=90^{\circ}
$$
Case 2: $A E P F$ and $C E P D$ are concyclic. Now by lemma 1 applied to the quadrilateral $A E P F$ we get that the circumcircles of $C E P, C A F, B P F$ and $B E A$ intersect at a point on $B C$. Since $D \in B C$ and $C E P D$ is concyclic we get that $D$ is the desired point and it follows that $B D P F, B A E D, C A F D$ are all concylic and now we can finish same as Case 1 since $A E D B$ and $C E P D$ are concyclic.
Case 3: $A E P F$ and $A E D B$ are concyclic. We apply lemma 1 as in Case 2 on the quadrilateral $A E P F$. From the lemma we get that $B D P F, C E P D$ and $C A F D$ are concylic and we finish off the same as in Case 1.
Case 4: $A C D F$ and $A B D E$ are concyclic. We apply lemma 1 on the quadrilateral $A E P F$ and get that the circumcircles of $A C F, E C P, P F B$ and $B A E$ intersect at one point. Since this point is $D$ (because $A C D F$ and $A B D E$ are concyclic) we get that $A E P F, C E P D$ and $B F P D$ are concylic. We now finish off as in Case 1. These four cases prove the problem statement.
Remark. A more natural approach is to solve each of the four cases by simple angle chasing.
## Number Theory
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 24 |
A2. Let $a, b, c$ be positive real numbers such that abc $=1$. Show that
$$
\frac{1}{a^{3}+b c}+\frac{1}{b^{3}+c a}+\frac{1}{c^{3}+a b} \leq \frac{(a b+b c+c a)^{2}}{6}
$$
so
|
Solution. By the AM-GM inequality we have $a^{3}+b c \geq 2 \sqrt{a^{3} b c}=2 \sqrt{a^{2}(a b c)}=2 a$ and
$$
\frac{1}{a^{3}+b c} \leq \frac{1}{2 a}
$$
Similarly; $\frac{1}{b^{3}+c a} \leq \frac{1}{2 b} \cdot \frac{1}{c^{3}+a b} \leq \frac{1}{2 c}$ and then
$$
\frac{1}{a^{3}+b c}+\frac{1}{b^{3}+c a}+\frac{1}{c^{3}+a b} \leq \frac{1}{2 a}+\frac{1}{2 b}+\frac{1}{2 c}=\frac{1}{2} \frac{a b+b c+c a}{a b c} \leq \frac{(a b+b c+c a)^{2}}{6}
$$
Therefore it is enongil to prove $\frac{(a h+b c+c a)^{2}}{6} \leq \frac{(a b+b c+c a)^{2}}{6}$. This mequalits is trivially shomn to be equivalent to $3 \leq a b+b c+c a$ which is true because of the AM-GM inequalit: $3=\sqrt[3]{(a b c)^{2}} \leq a b+b c+c a$.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 25 |
A3. Let $a . b$ c ce positue real numbers such that $a+b+c=a^{2}+b^{2}+c^{2}$. Shou that
$$
\frac{a^{2}}{a^{2}+a b}+\frac{b^{2}}{b^{2}+b c}+\frac{c^{2}}{c^{2}+c a} \geq \frac{a+b+c}{2}
$$
|
Solution. By the Cauchy-Schwarz inequality it is
$$
\begin{aligned}
& \left(\frac{a^{2}}{a^{2}+a b}+\frac{b^{2}}{b^{2}+b c}+\frac{c^{2}}{c^{2}+c a}\right)\left(\left(a^{2}+a b\right)+\left(b^{2}+b c\right)+\left(c^{2}+c a\right)\right) \geq(a+b+c)^{2} \\
\Rightarrow & \frac{a^{2}}{a^{2}+a b}+\frac{b^{2}}{b^{2}+b c}+\frac{c^{2}}{c^{2}+c a} \geq \frac{(a+b+c)^{2}}{a^{2}+b^{2}+c^{2}+a b+b c+c a}
\end{aligned}
$$
So in is enough to prove $\frac{(a+b+c)^{2}}{a^{2}+b^{2}+c^{2}+a b+b c+c a} \geq \frac{a+b+c}{2}$, that is to prove
$$
2(a+b+c) \geq a^{2}+b^{2}+c^{2}+a b+b c+c a
$$
Substituting $a^{2}+b^{2}+c^{2}$ for $a+b+c$ into the left hand side we wish equivalently to prove
$$
a^{2}+b^{2}+c^{2} \geq a b+b c+c a
$$
But the $a^{2}+b^{2} \geq 2 a b, b^{2}+c^{2} \geq 2 b c, c^{2}+a^{2} \geq 2 c a$ which by addition imply the desired inequality.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 26 |
G1. Let $A B C$ be an equilateral triangle, and $P$ a point on the circumcircle of the triangle $A B C$ and distinct from $A, B$ and $C$. If the lines through $P$ and parallel to $B C, C A, A B$ intersect the lines $C A, A B, B C$ at $M, N$ and $Q$ respectively, prove that $M, N$ and $Q$ are collinear.
|
Solution. Without any loss of generality, let $P$ be in the minor arc of the chord $A C$ as in Figure 1. Since $\angle P N A=\angle N P M=60^{\circ}$ and $\angle N A M=\angle P M A=120^{\circ}$, it follows that the points $A, M, P$ and $N$ are concyclic. This yields
$$
\angle N M P=\angle N A P
$$
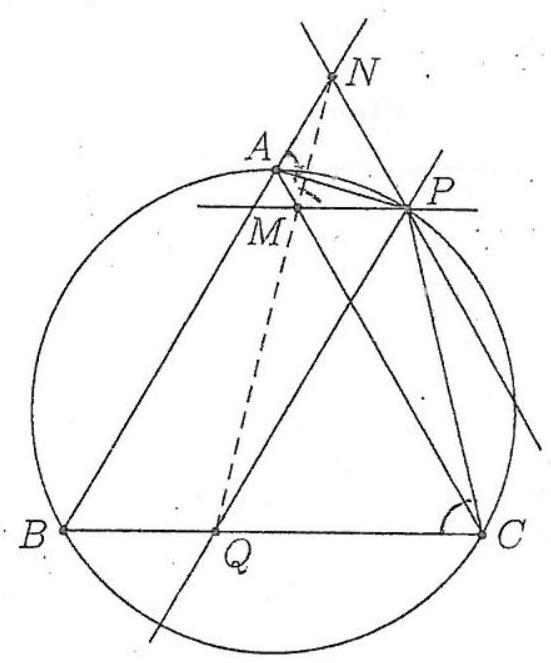
Figure 1: Exercise G1.
Similarly, since $\angle P M C=\angle M C Q=60^{\circ}$ and $\angle C Q P=60^{\circ}$, it follows that the points $P, M, Q$ and $C$ are concyclic. Thus
$$
\angle P M Q=180^{\circ}-\angle P C Q=180^{\circ}-\angle N A P \stackrel{(2)}{=} 180^{\circ}-\angle N M P .
$$
This implies $\angle P M Q+\angle N M P=180^{\circ}$, which shows that $M, N$ and $Q$ belong to the same line.
1 G2. Let $A B C$ be an isosceles triangle with $A B=A C$. Let also $c(K, K C)$ be a circle tangent to the line $A C$ at point $C$ which it intersects the segment $B C$ again at an interior point $H$. Prove that $H K \perp A B$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 27 |
C3. In a circle of diameter 1 consider 65 points no three of which are collinear. Prove that there exist 3 among these points which form a triangle with area less then or equal to $\frac{1}{72}$.
|
Solution. Lemma: If a triangle $A B C$ lies in a rectangle $K L M N$. with sides $K L=a$ and $L M=b$, then the area of the triangle is less then or equal to $\frac{a b}{2}$.
Proof of the lemma: Writhout any loss of generality assume that among the distance of $A, B, C$ from $K L$, that of $A$ is between the other two. Let $\ell$ be the line through $A$ and parallel to $K L$. Let $D$ be the intersection of $\ell, B C$ and $x, y$ the distances of $B, C$ from $\ell$ respectively. Then the area of $A B C$ equals $\frac{A D(x+y)}{2} \leq \frac{a b}{2}$, since $A D \leq a$ and $x+y \leq b$ and we are done.
Now back to our problem, let us cover the circle with 24 squares of side $\frac{1}{6}$ and 8 other irregular and equal figures as shown in Figure 9, with boundary consisting of an arc on the circle and three line segments. Call $S=A D N M$ one of these figures. One of the line segments in the boundary of $S$ is of length $A D=A B-D B=\sqrt{A C^{2}-B C^{2}}-\frac{2}{6}=$ $\sqrt{\left(\frac{1}{2}\right)^{2}-\left(\frac{1}{6}\right)^{2}}-\frac{1}{3}=\frac{\sqrt{2}-1}{3}$. The boundary segment $M N$ goes through the center $C$ of the circle, forming with the horizontal lines an angle of $45^{\circ}$. The point in $S$ with maximum distance from the boundary segment $A B$ is the endpoint $M$ of the arc on the boundary of $S$. This distance equals $M E=M F-E F \stackrel{C M F=\text { isosceles }}{=} \frac{\sqrt{2}}{2} C M-\frac{1}{6}=\frac{\sqrt{2}}{4}-\frac{1}{6}=\frac{3 \sqrt{2}-2}{12}$. So $S$ can be put inside a rectangle $R$ with sides parallel to $A D, N D$ of lengths $\frac{\sqrt{2}-1}{3}$ and $\frac{3 \sqrt{2}-2}{12}$. So the triangle formed by any three points inside this figure, has an area less or
equal to $\frac{1}{2} \cdot \frac{\sqrt{2}-1}{3} \cdot \frac{3 \sqrt{2}-2}{12}=\frac{8-5 \sqrt{2}}{72}<\frac{1}{72}$.
Also, the triangle formed by any three points inside any square of side $\frac{1}{6}$, has an area less or equal to $\frac{1}{2} \cdot \frac{1}{6} \cdot \frac{1}{6}=\frac{1}{72}$.
By the Pigeonhole Principle, we know that among the 65 given points there exist 3 inside the same one of the 32 squares and irregular figures of the picture covering the given circle. Then according to the above, the triangle formed by these 3 points has an area not exceeding $\frac{1}{72}$ as wanted.
Figure 9: :Exercise C3.
## Number Theory
3 NT1. If $a, b$ are integers and $s=a^{3}+b^{3}-60 a b(a+b) \geq 2012$, find the least possible value of $s$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 28 |
A3. Show that
$$
\left(a+2 b+\frac{2}{a+1}\right)\left(b+2 a+\frac{2}{b+1}\right) \geq 16
$$
for all positive real numbers $a, b$ satisfying $a b \geq 1$.
|
Solution 1. By the AM-GM Inequality we have:
$$
\frac{a+1}{2}+\frac{2}{a+1} \geq 2
$$
Therefore
$$
a+2 b+\frac{2}{a+1} \geq \frac{a+3}{2}+2 b
$$
and, similarly,
$$
b+2 a+\frac{2}{b+1} \geq 2 a+\frac{b+3}{2}
$$
On the other hand,
$$
(a+4 b+3)(b+4 a+3) \geq(\sqrt{a b}+4 \sqrt{a b}+3)^{2} \geq 64
$$
by the Cauchy-Schwarz Inequality as $a b \geq 1$, and we are done.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 29 |
G1. Let $A B$ be a diameter of a circle $\omega$ with center $O$ and $O C$ be a radius of $\omega$ which is perpendicular to $A B$. Let $M$ be a point on the line segment $O C$. Let $N$ be the second point of intersection of the line $A M$ with $\omega$, and let $P$ be the point of intersection of the lines tangent to $\omega$ at $N$ and at $B$. Show that the points $M, O, P, N$ are concyclic.
|
Solution. Since the lines $P N$ and $B P$ are tangent to $\omega, N P=P B$ and $O P$ is the bisector of $\angle N O B$. Therefore the lines $O P$ and $N B$ are perpendicular. Since $\angle A N B=90^{\circ}$, it follows that the lines $A N$ and $O P$ are parallel. As $M O$ and $P B$ are also parallel and $A O=O B$, the triangles $A M O$ and $O P B$ are congruent and $M O=P B$. Hence $M O=N P$. Therefore $M O P N$ is an isosceles trapezoid and therefore cyclic. Hence the points $M, O, P, N$ are concyclic.
8.2. $\omega_{1}$ and $\omega_{2}$ are two circles that are externally tangent to each other at the point $M$ and internally tangent to a circle $\omega_{3}$ at the points $K$ and $L$, respectively. Let $A$ and $B$ be the two points where the common tangent line at $M$ to $\omega_{1}$ and $\omega_{2}$ intersects $\omega_{3}$. Show that if $\angle K A B=\angle L A B$ then the line segment $A B$ is a diameter of $\omega_{3}$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 30 |
G3. Let $D$ be a point on the side $B C$ of an acute triangle $A B C$ such that $\angle B A D=\angle C A O$ where $O$ is the center of the circumcircle $\omega$ of the triangle $A B C$. Let $E$ be the second point of intersection of $\omega$ and the line $A D$. Let $M, N, P$ be the midpoints of the line segments $B E, O D, A C$, respectively. Show that $M, N, P$ are collinear.
|
Solution. We will show that $M O P D$ is a parallelogram. From this it follows that $M, N$, $P$ are collinear.
Since $\angle B A D=\angle C A O=90^{\circ}-\angle A B C, D$ is the foot of the perpendicular from $A$ to side $B C$. Since $M$ is the midpoint of the line segment $B E$, we have $B M=M E=M D$ and hence $\angle M D E=\angle M E D=\angle A C B$.
Let the line $M D$ intersect the line $A C$ at $D_{1}$. Since $\angle A D D_{1}=\angle M D E=\angle A C D, M D$ is perpendicular to $A C$. On the other hand, since $O$ is the center of the circumcircle of triangle $A B C$ and $P$ is the midpoint of the side $A C, O P$ is perpendicular to $A C$. Therefore $M D$ and $O P$ are parallel.
Similarly, since $P$ is the midpoint of the side $A C$, we have $A P=P C=D P$ and hence $\angle P D C=\angle A C B$. Let the line $P D$ intersect the line $B E$ at $D_{2}$. Since $\angle B D D_{2}=\angle P D C=$ $\angle A C B=\angle B E D$, we conclude that $P D$ is perpendicular to $B E$. Since $M$ is the midpoint of the line segment $B E, O M$ is perpendicular to $B E$ and hence $O M$ and $P D$ are parallel.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 31 |
G4. Let $I$ be the incenter and $A B$ the shortest side of a triangle $A B C$. The circle with center $I$ and passing through $C$ intersects the ray $A B$ at the point $P$ and the ray $B A$ at the point $Q$. Let $D$ be the point where the excircle of the triangle $A B C$ belonging to angle $A$ touches the side $B C$, and let $E$ be the symmetric of the point $C$ with respect to $D$. Show that the lines $P E$ and $C Q$ are perpendicular.
|
Solution. First we will show that points $P$ and $Q$ are not on the line segment $A B$.
Assume that $Q$ is on the line segment $A B$. Since $C I=Q I$ and $\angle I B Q=\angle I B C$, either the triangles $C B I$ and $Q B I$ are congruent or $\angle I C B+\angle I Q B=180^{\circ}$. In the first case, we have $B C=B Q$ which contradicts $A B$ being the shortest side.
In the second case, we have $\angle I Q A=\angle I C B=\angle I C A$ and the triangles $I A C$ and $I A Q$ are congruent. Hence this time we have $A C=A Q$, contradicting $A B$ being the shortest side.
Case 1
Now we will show that the lines $P E$ and $C Q$ are perpendicular.
Since $\angle I Q B \leq \angle I A B=(\angle C A B) / 2<90^{\circ}$ and $\angle I C B=(\angle A C B) / 2<90^{\circ}$, the triangles $C B I$ and $Q B I$ are congruent. Hence $B C=B Q$ and $\angle C Q P=\angle C Q B=90^{\circ}-(\angle A B C) / 2$. Similarly, we have $A C=A P$ and hence $B P=A C-A B$.
On the other hand, as $D E=C D$ and $C D+A C=u$, where $u$ denotes the semiperimeter of the triangle $A B C$, we have $B E=B C-2(u-A C)=A C-A B$. Therefore $B P=B E$ and $\angle Q P E=(\angle A B C) / 2$.
Hence, $\angle C Q P+\angle Q P E=90^{\circ}$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 32 |
G5. A circle passing through the midpoint $M$ of the side $B C$ and the vertex $A$ of a triangle $A B C$ intersects the sides $A B$ and $A C$ for the second time at the points $P$ and $Q$, respectively. Show that if $\angle B A C=60^{\circ}$ then
$$
A P+A Q+P Q<A B+A C+\frac{1}{2} B C
$$
|
Solution. Since the quadrilateral $A P M Q$ is cyclic, we have $\angle P M Q=180^{\circ}-\angle P A Q=$ $180^{\circ}-\angle B A C=120^{\circ}$. Therefore $\angle P M B+\angle Q M C=180^{\circ}-\angle P M Q=60^{\circ}$.
Let the point $B^{\prime}$ be the symmetric of the point $B$ with respect to the line $P M$ and the point $C^{\prime}$ be the symmetric of the point $C$ with respect to the line $Q M$. The triangles $B^{\prime} M P$ and $B M P$ are congruent and the triangles $C^{\prime} M Q$ and $C M Q$ are congruent. Hence $\angle B^{\prime} M C^{\prime}=\angle P M Q-\angle B^{\prime} M P-\angle C^{\prime} M Q=120^{\circ}-\angle B M P-\angle C M Q=120^{\circ}-60^{\circ}=60^{\circ}$. As we also have $B^{\prime} M=B M=C M=C^{\prime} M$, we conclude that the triangle $B^{\prime} M C^{\prime}$ is equilateral and $B^{\prime} C^{\prime}=B C / 2$.
On the other hand, we have $P B^{\prime}+B^{\prime} C^{\prime}+C^{\prime} Q \geq P Q$ by the Triangle Inequality, and hence $P B+B C / 2+Q C \geq P Q$. This gives the inequality $A B+B C / 2+A C \geq A P+P Q+A Q$.
We get an equality only when the points $B^{\prime}$ and $C^{\prime}$ lie on the line segment $P Q$. If this is the case, then $\angle P Q C+\angle Q P B=2(\angle P Q M+\angle Q P M)=120^{\circ}$ and therefore $\angle A P Q+\angle A Q P=$ $240^{\circ} \neq 120^{\circ}$, a contradiction.
$A B C D$. Let $K$ and $M$ be the points of intersection of the line $P D$ with $Q B$ and $Q A$, respectively, and let $N$ be the point of intersection of the lines $P A$ and $Q B$.
Let $X, Y, Z$ be the midpoints of the line segments $A N, K N, A M$, respectively. Let $\ell_{1}$ be the line passing through $X$ and perpendicular to $M K, \ell_{2}$ be the line passing through $Y$ and perpendicular to $A M, \ell_{3}$ be the line passing through $Z$ and perpendicular to $K N$. Show that $\ell_{1}, \ell_{2}, \ell_{3}$ are concurrent.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 33 |
## A5 MKCD
Let $x, y, z$ be positive real numbers that satisfy the equality $x^{2}+y^{2}+z^{2}=3$. Prove that
$$
\frac{x^{2}+y z}{x^{2}+y z+1}+\frac{y^{2}+z x}{y^{2}+z x+1}+\frac{z^{2}+x y}{z^{2}+x y+1} \leq 2
$$
|
## Solution:
We have
$$
\begin{aligned}
& \frac{x^{2}+y z}{x^{2}+y z+1}+\frac{y^{2}+z x}{y^{2}+z x+1}+\frac{z^{2}+x y}{z^{2}+x y+1} \leq 2 \Leftrightarrow \\
& \frac{x^{2}+y z+1}{x^{2}+y z+1}+\frac{y^{2}+z x+1}{y^{2}+z x+1}+\frac{z^{2}+x y+1}{z^{2}+x y+1} \leq 2+\frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \Leftrightarrow \\
& 3 \leq 2+\frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \Leftrightarrow \\
& 1 \leq \frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \\
& \frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \geq \frac{9}{x^{2}+y z+1+y^{2}+z x+1+z^{2}+x y+1}= \\
& \frac{9}{x^{2}+y^{2}+z^{2}+x y+y z+z x+3} \geq \frac{9}{2 x^{2}+y^{2}+z^{2}+3}=1
\end{aligned}
$$
The first inequality: AM-GM inequality (also can be achieved with Cauchy-BunjakowskiSchwarz inequality). The second inequality: $x y+y z+z x £ x^{2}+y^{2}+z^{2}$ (there are more ways to prove it, AM-GM, full squares etc.)
## GEOMETRY
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 35 |
## G1 MNE
Around the triangle $A B C$ the circle is circumscribed, and at the vertex $C$ tangent $t$ to this circle is drawn. The line $p$ which is parallel to this tangent intersects the lines $B C$ and $A C$ at the points $D$ and $E$, respectively. Prove that the points $A, B, D, E$ belong to the same circle.
|
## Solution:
Let $O$ be the center of a circumscribed circle $k$ of the triangle $A B C$, and let $F$ and $G$ be the points of intersection of the line $C O$ with the line $p$ and the circle $k$, respectively (see Figure). From $p \| t$ it follows that $p \perp C O$. Furthermore, $\angle A B C=\angle A G C$, because these angles are peripheral over the same chord. The quadrilateral $A G F E$ has two right angles at the vertices $A$ and $F$, and hence, $\angle A E D+\angle A B D=\angle A E F+\angle A G F=180^{\circ}$. Hence, the quadrilateral $A B D E$ is cyclic, as asserted.
Figure
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 36 |
## G2 MLD
The point $P$ is outside of the circle $\Omega$. Two tangent lines, passing from the point $P$, touch the circle $\Omega$ at the points $A$ and $B$. The median $A M, M \in(B P)$, intersects the circle $\Omega$ at the point $C$ and the line $P C$ intersects again the circle $\Omega$ at the point $D$. Prove that the lines $A D$ and $B P$ are parallel.
|
## Solution:
Since $\angle B A C=\angle B A M=\angle M B C$, we have $\triangle M A B \cong \triangle M B C$.
We obtain $\frac{M A}{M B}=\frac{M B}{M C}=\frac{A B}{B C}$. The equality $\quad M B=M P$ implies $\frac{M A}{M P}=\frac{M P}{M C}$ and $\angle P M C \equiv \angle P M A$ gives the relation $\triangle P M A \cong \triangle C M P$. It follows that $\angle B P D \equiv \angle M P C \equiv \angle M A P \equiv \angle C A P \equiv \angle C D A \equiv \angle P D A$. So, the lines $A D$ and $B P$ are parallel.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 37 |
## G3 GRE
Let $c \equiv c(O, K)$ be a circle with center $O$ and radius $R$ and $A, B$ be two points on it, not belonging to the same diameter. The bisector of the angle $A \hat{B} O$ intersects the circle $c$ at point $C$, the circumcircle of the triangle $A O B$, say ${ }^{c_{1}}$ at point $K$ and the circumcircle of the triangle $A O C$, say ${ }^{c_{2}}$, at point $L$. Prove that the point $K$ is the circumcenter of the triangle $A O C$ and the point $L$ is the incenter of the triangle $A O B$.
|
## Solution:
The segments $O B, O C$ are equal, as radii of the circle ${ }^{c}$. Hence $O B C$ is an isosceles triangle and
$$
\hat{B}_{1}=\hat{C}_{1}=\hat{x}
$$
The chord $B C$ is the bisector of the angle $O \hat{B} A$, and hence
$$
\hat{B}_{1}=\hat{B}_{2}=\hat{x}
$$
The angles $\hat{B}_{2}$ and $\hat{O}_{1}$ are inscribed to the same arc $O K$ of the circle ${ }^{c_{1}}$ and hence
$$
\hat{B}_{2}=\hat{\mathrm{O}}_{1}=\hat{x}
$$
The segments $K O, K C$ are equal, as radii of the circle ${ }^{c_{2}}$. Hence the triangle $K O C$ is isosceles and so
$$
\hat{O}_{2}=\hat{C}_{1}=\hat{x}
$$
From equalities $(1),(2),(3)$ we conclude that
$$
\hat{O}_{1}=\hat{O}_{2}=\hat{x}
$$
and so $O K$ is the bisector, and hence perpendicular bisector of the isosceles triangle $O A C$. The point $K$ is the middle of the arc $O K$ (since $B K$ bisects the angle $O \hat{B} A$ ). Hence the perpendicular bisector of the chord $A O$ of the circle ${ }^{c_{1}}$ is passing through point $K$. It means that $K$ is the circumcenter of the triangle $O A C$.
From equalities (1),(2),(3) we conclude that $\hat{B}_{2}=\hat{C}_{1}=\hat{x}$ and so $A B / / O C \Rightarrow O \hat{A} B=A \hat{O} C$, that is $\hat{A}_{1}+\hat{A}_{2}=\hat{O}_{1}+\hat{O}_{2}$ and since $\hat{O}_{1}=\hat{O}_{2}=\hat{x}$, we conclude that
$$
\hat{A}_{1}+\hat{A}_{2}=2 \hat{O}_{1}=2 \hat{x}
$$
The angles $\hat{A}_{I}$ and $\hat{C}_{I}$ are inscribed into the circle ${ }^{c_{2}}$ and correspond to the same arc $O L$. Hence
$$
\hat{A}_{I}=\hat{C}_{1}=\hat{x}
$$
From (5) and (6) we have $\hat{A}_{1}=\hat{A}_{2}$, i.e. $A L$ is the bisector of the angle $B \hat{A} O$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 38 |
G4
CYP
Let $\triangle A B C$ be an acute triangle. The lines $\left(\varepsilon_{1}\right),\left(\varepsilon_{2}\right)$ are perpendicular to $A B$ at the points $A$, $B$, respectively. The perpendicular lines from the midpoint $M$ of $A B$ to the sides of the triangle $A C_{;} B C$ intersect the lines $\left(\varepsilon_{1}\right),\left(\xi_{2}\right)$ at the points $E, F$, respectively. If $I$ is the intersection point of $E F, M C$, prove that
$$
\angle A I B=\angle E M F=\angle C A B+\angle C B A
$$
|
## Solution:
Let $H, G$ be the points of intersection of $M E, M F$, with $A C, B C$ respectively. From the similarity of triangles $\triangle M H A$ and $\triangle M A E$ we get
$$
\frac{M H}{M A}=\frac{M A}{M E}
$$
thus, $M A^{2}=M H \cdot M E$
Similarly, from the similarity of triangles $\triangle M B G$ and $\triangle M F B$ we get
$$
\frac{M B}{M F}=\frac{M G}{M B}
$$
thus, $M B^{2}=M F \cdot M G$
Since $M A=M B$, from (1), (2), we have that the points $E, H, G, F$ are concyclic.
Therefore, we get that $\angle F E H=\angle F E M=\angle H G M$. Also, the quadrilateral $C H M G$ is cyclic, so $\angle C M H=\angle H G C$. We have
$$
\angle F E H+\angle C M H=\angle H G M+\angle H G C=90^{\circ}
$$
Thus $C M \perp E F$. Now, from the cyclic quadrilaterals $F I M B$ and EIMA, we get that
$\angle I F M=\angle I B M$ and $\angle I E M=\angle I A M$. Therefore, the triangles $\triangle E M F$ and $\triangle A I B$ are similar, so $\angle A J B=\angle E M F$. Finally
$$
\angle A I B=\angle A I M+\angle M I B=\angle A E M+\angle M F B=\angle C A B+\angle C B A
$$
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 39 |
G5 ROU
Let $A B C$ be an acute triangle with $A B \neq A C$. The incircle $\omega$ of the triangle touches the sides $B C, C A$ and $A B$ at $D, E$ and $F$, respectively. The perpendicular line erected at $C$ onto $B C$ meets $E F$ at $M$, and similarly, the perpendicular line erected at $B$ onto $B C$ meets $E F$ at $N$. The line $D M$ meets $\omega$ again in $P$, and the line $D N$ meets $\omega$ again at $Q$. Prove that $D P=D Q$.
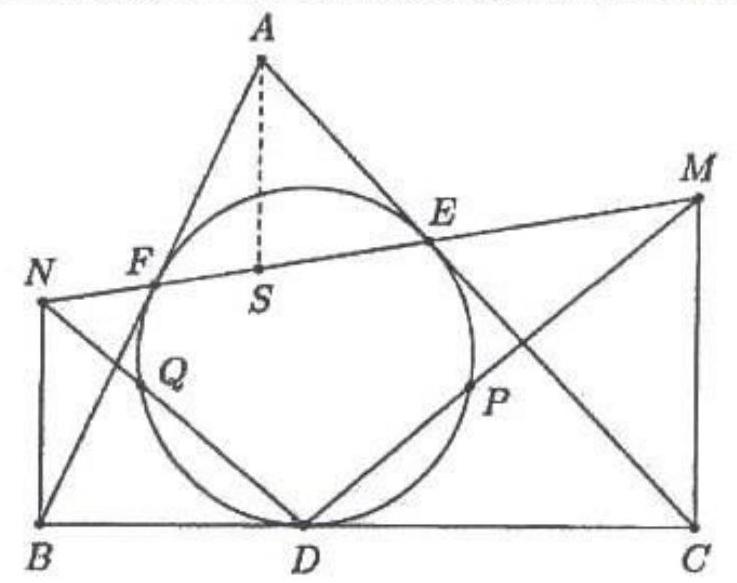
|
## Solution:
## Proof 1.1.
Let $\{T\}=E F \cap B C$. Applying Menelaus' theorem to the triangle $A B C$ and the transversal line $E-F-T$ we obtain $\frac{T B}{T C} \cdot \frac{E C}{E A} \cdot \frac{F A}{F B}=1$, i.e. $\frac{T B}{T C} \cdot \frac{s-c}{s-a} \cdot \frac{s-a}{s-b}=1$, or $\frac{T B}{T C}=\frac{s-b}{s-c}$, where the notations are the usual ones.
This means that triangles $T B N$ and $T C M$ are similar, therefore $\frac{T B}{T C}=\frac{B N}{C M}$. From the above it follows $\frac{B N}{C M}=\frac{s-b}{s-c}, \frac{B D}{C D}=\frac{s-b}{s-c}$, and $\angle D B N=\angle D C M=90^{\circ}$, which means that triangles $B D N$ and $C D M$ are similar, hence angles $B D N$ and $C D M$ are equal. This leads to the arcs $D Q$ and $D P$ being equal, and finally to $D P=D Q$.
## Proof 1.2.
Let $S$ be the meeting point of the altitude from $A$ with the line $E F$. Lines $B N, A S, C M$ are parallel, therefore triangles $B N F$ and $A S F$ are similar, as are triangles $A S E$ and $C M E$. We obtain $\frac{B N}{A S}=\frac{B F}{F A}$ and $\frac{A S}{C M}=\frac{A E}{E C}$.
Multiplying the two relations, we obtain $\frac{B N}{C M}=\frac{B F}{F A} \cdot \frac{A E}{E C}=\frac{B F}{E C}=\frac{B D}{D C}$ (we have used that $A E=A F, B F=B D$ and $C E=C D)$.
It follows that the right triangles $B D N$ and $C D M$ are similar (SAS), which leads to the same ending as in the first proof.
## NUMBER THEORY
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 40 |
NT2 BUL
A positive integer is called a repunit, if it is written only by ones. The repunit with $n$ digits will be denoted by $\underbrace{11 \ldots 1}_{n}$. Prove that:
a) the repunit $\underbrace{11 \ldots 1}_{n}$ is divisible by 37 if and only if $n$ is divisible by 3 ;
b) there exists a positive integer $k$ such that the repunit $\underbrace{11 \ldots 1}_{n}$ is divisible by 41 if and only if $n$ is divisible by $k$.
|
## Solution:
a) Let $n=3 m+r$, where $m$ and $r$ are non-negative integers and $r<3$.
Denote by $\underbrace{00 \ldots 0}_{p}$ a recording with $p$ zeroes and $\underbrace{a b c a b c \ldots a b c}_{p x a b c c}$ recording with $p$ times $a b c$. We
have: $\quad \underbrace{11 \ldots 1}_{n}=\underbrace{11 \ldots 1}_{3 m+r}=\underbrace{11 \ldots 1}_{3 m} \cdot \underbrace{00 \ldots 0}_{r}+\underbrace{11 \ldots 1}_{\tau}=111 \cdot \underbrace{100100 \ldots 100100 \ldots 0}_{(m-1) \times 100}+\underbrace{11 \ldots 1}_{r}$.
Since $111=37.3$, the numbers $\underbrace{11 \ldots 1}_{n}$ and $\underbrace{11 \ldots 1}_{r}$ are equal modulo 37 . On the other hand the numbers 1 and 11 are not divisible by 37 . We conclude that $\underbrace{11 \ldots 1}_{n}$ is divisible by 37 if only if $r=0$, i.e. if and only if $n$ is divisible by 3 .
b) Using the idea from a), we look for a repunit, which is divisible by 41 . Obviously, 1 and 11 are not divisible by 41 , while the residues of 111 and 1111 are 29 and 4 , respectively. We have $11111=41 \cdot 271$. Since 11111 is a repunit with 5 digits, it follows in the same way as in a) that $\underbrace{1}_{11 \ldots 1}$ is divisible by 41 if and only if $n$ is divisible by 5 .
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 41 |
## NT3 ALB
a) Show that the product of all differences of possible couples of six given positive integers is divisible by 960 (original from Albania).
b) Show that the product of all differences of possible couples of six given positive integers. is divisible by 34560 (modified by problem selecting committee).
|
## Solution:
a) Since we have six numbers then at least two of them have a same residue when divided by 3 , so at least one of the differences in our product is divisible by 3 .
Since we have six numbers then at least two of them have a same residuc when divided by 5 , so at least one of the differences in our product is divisible by 5 .
We may have:
a) six numbers with the same parity
b) five numbers with the same parity
c) four numbers with the same parity
d) three numbers with the same parity
There are $C_{6}^{2}=15$ different pairs, so there are 15 different differences in this product.
a) The six numbers have the same parity; then each difference is divisible by 2 , therefore our product is divisible by $2^{15}$.
b) If we have five numbers with the same parity, then the couples that have their difference odd are formed by taking one number from these five numbers, and the second will be the sixth one. Then $C_{5}^{1}=15=5$ differences are odd. So $15-5=10$ differences are even, so product is divisible by $2^{10}$.
c) If we have four numbers with the same parity, then the couples that have their difference odd are formed by taking one number from these four numbers, and the second will be from the two others numbers. Then $2 \cdot C_{4}^{1}=8$ differences are odd. So $15-8=7$ differences are even, so our product is divisible by $2^{7}$.
d) If we have three numbers with the same parity, then the couples that have their difference odd are formed by taking one from each triple. Then $C_{3}^{1} \cdot C_{3}^{1}=9$ differences are odd, therefore $15-9=6$ differences are even, so our product is divisible by $2^{6}$.
Thus, our production is divisible by $2^{6} \cdot 3 \cdot 5=960$.
b) Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}$ be these numbers. Since we have six numbers then at least two of them when divided by 5 have the same residue, so at least one of these differences in our product is divisible by 5 .
Since we have six numbers, and we have three possible residues at the division by 3 , then at least three of them replies the residue of previous numbers, so at least three of these differences in our product are divisible by 3 .
Since we have six numbers, and we have two possible residues at the division by 2 , then at least four of them replies the residue of previous numbers, and two of them replies replied residues, so at least six of these differences in our product are divisible by 2 .
Since we have six numbers, and we have four possible residues at the division by 4 , then at least two of them replies the residue of previous numbers, so at least two of these differences in our product are divisible by 4 . That means that two of these differences are divisible by 4 and moreover four of them are divisible by 2 .
Thus, our production is divisible by $2^{4} \cdot 4^{2} \cdot 3^{3} \cdot 5=34560$.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 42 |
A1 Let $a$ be a real positive number such that $a^{3}=6(a+1)$. Prove that the equation $x^{2}+a x+a^{2}-6=0$ has no solution in the set of the real number.
|
## Solution
The discriminant of the equation is $\Delta=3\left(8-a^{2}\right)$. If we accept that $\Delta \geq 0$, then $a \leq 2 \sqrt{2}$ and $\frac{1}{a} \geq \frac{\sqrt{2}}{4}$, from where $a^{2} \geq 6+6 \cdot \frac{\sqrt{2}}{4}=6+\frac{6}{a} \geq 6+\frac{3 \sqrt{2}}{2}>8$ (contradiction).
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 43 |
A2 Prove that $\frac{a^{2}-b c}{2 a^{2}+b c}+\frac{b^{2}-c a}{2 b^{2}+c a}+\frac{c^{2}-a b}{2 c^{2}+a b} \leq 0$ for any real positive numbers $a, b, c$.
|
## Solution
The inequality rewrites as $\sum \frac{2 a^{2}+b c-3 b c}{2 a^{2}+b c} \leq 0$, or $3-3 \sum \frac{b c}{2 a^{2}+b c} \leq 0$ in other words $\sum \frac{b c}{2 a^{2}+b c} \geq 1$.
Using Cauchy-Schwarz inequality we have
$$
\sum \frac{b c}{2 a^{2}+b c}=\sum \frac{b^{2} c^{2}}{2 a^{2} b c+b^{2} c^{2}} \geq \frac{\left(\sum b c\right)^{2}}{2 a b c(a+b+c)+\sum b^{2} c^{2}}=1
$$
as claimed.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 44 |
A3 Let $A$ be a set of positive integers containing the number 1 and at least one more element. Given that for any two different elements $m, n$ of $A$ the number $\frac{m+1}{(m+1, n+1)}$ is also an element of $A$, prove that $A$ coincides with the set of positive integers.
|
## Solution
Let $a>1$ be lowest number in $A \backslash\{1\}$. For $m=a, n=1$ one gets $y=\frac{a+1}{(2, a+1)} \in A$. Since $(2, a+1)$ is either 1 or 2 , then $y=a+1$ or $y=\frac{a+1}{2}$.
But $1<\frac{a+1}{2}<a$, hence $y=a+1$. Applying the given property for $m=a+1, n=a$ one has $\frac{a+2}{(a+2, a+1)}=a+2 \in A$, and inductively $t \in A$ for all integers $t \geq a$.
Furthermore, take $m=2 a-1, n=3 a-1$ (now in $A!$ ); as $(m+1, n+1)=(2 a, 3 a)=a$ one obtains $\frac{2 a}{a}=2 \in A$, so $a=2$, by the definition of $a$.
The conclusion follows immediately.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 45 |
A4 Let $a$ and $b$ be positive integers bigger than 2. Prove that there exists a positive integer $k$ and a sequence $n_{1}, n_{2}, \ldots, n_{k}$ consisting of positive integers, such that $n_{1}=a$, $n_{k}=b$, and $\left(n_{i}+n_{i+1}\right) \mid n_{i} n_{i+1}$ for all $i=1,2, \ldots, k-1$.
|
## Solution
We write $a \Leftrightarrow b$ if the required sequence exists. It is clear that $\Leftrightarrow$ is equivalence relation, i.e. $a \Leftrightarrow a,(a \Leftrightarrow b$ implies $b \Rightarrow a)$ and $(a \Leftrightarrow b, b \Leftrightarrow c$ imply $a \Leftrightarrow c$ ).
We shall prove that for every $a \geq 3$, ( $a-$ an integer), $a \Leftrightarrow 3$.
If $a=2^{s} t$, where $t>1$ is an odd number, we take the sequence
$$
2^{s} t, 2^{s}\left(t^{2}-t\right), 2^{s}\left(t^{2}+t\right), 2^{s}(t+1)=2^{s+1} \cdot \frac{t+1}{2}
$$
Since $\frac{t+1}{2}1$ we have $2^{s}, 3 \cdot 2^{s}, 3 \cdot 2^{s-1}, 3 \cdot 2^{s-2}, \ldots, 3$.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 46 |
A5 The real numbers $x, y, z, m, n$ are positive, such that $m+n \geq 2$. Prove that
$$
\begin{gathered}
x \sqrt{y z(x+m y)(x+n z)}+y \sqrt{x z(y+m x)(y+n z)}+z \sqrt{x y(z+m x)(x+n y)} \leq \\
\frac{3(m+n)}{8}(x+y)(y+z)(z+x) .
\end{gathered}
$$
|
## Solution
Using the AM-GM inequality we have
$$
\begin{aligned}
& \sqrt{y z(x+m y)(x+n z)}=\sqrt{(x z+m y z)(x y+n y z)} \leq \frac{x y+x z+(m+n) y z}{2} \\
& \sqrt{x z(y+m x)(y+n z)}=\sqrt{(y z+m x z)(x y+n x z)} \leq \frac{x y+y z+(m+n) x z}{2} \\
& \sqrt{x y(z+m x)(z+n y)}=\sqrt{(y z+m x y)(x z+n x y)} \leq \frac{x z+y z+(m+n) x y}{2}
\end{aligned}
$$
Thus it is enough to prove that
$$
\begin{aligned}
x[x y+x z+(m+n) y z] & +y[x y+y z+(m+n) x z]+z[x y+y z+(m+n) x z] \leq \\
\leq & \frac{3(m+n)}{4}(x+y)(y+z)(z+x),
\end{aligned}
$$
or
$$
4[A+3(m+n) B] \leq 3(m+n)(A+2 B) \Leftrightarrow 6(m+n) B \leq[3(m+n)-4] A
$$
where $A=x^{2} y+x^{2} z+x y^{2}+y^{2} z+x z^{2}+y z^{2}, B=x y z$.
Because $m+n \geq 2$ we obtain the inequality $m+n \leq 3(m+n)-4$. From AMGM inequality it follows that $6 B \leq A$. From the last two inequalities we deduce that $6(m+n) B \leq[3(m+n)-4] A$. The inequality is proved.
Equality holds when $m=n=1$ and $x=y=z$.
### 2.2 Combinatorics
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 47 |
C1 We call a tiling of an $m \times n$ rectangle with corners (see figure below) "regular" if there is no sub-rectangle which is tiled with corners. Prove that if for some $m$ and $n$ there exists a "regular" tiling of the $m \times n$ rectangular then there exists a "regular" tiling also for the $2 m \times 2 n$ rectangle.
|
## Solution
A corner-shaped tile consists of 3 squares. Let us call "center of the tile" the square that has two neighboring squares. Notice that in a "regular" tiling, the squares situated in the corners of the rectangle have to be covered by the "center" of a tile, otherwise a $2 \times 3$ (or $3 \times 2$ ) rectangle tiled with two tiles would form.
Consider a $2 m \times 2 n$ rectangle, divide it into four $m \times n$ rectangles by drawing its midlines, then do a "regular" tiling for each of these rectangles. In the center of the $2 m \times 2 n$ rectangle we will necessarily obtain the following configuration:

Now simply change the position of these four tiles into:
It is easy to see that this tiling is "regular".
|
proof
|
Combinatorics
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 48 |
G1 Let $M$ be an interior point of the triangle $A B C$ with angles $\varangle B A C=70^{\circ}$ and $\varangle A B C=80^{\circ}$. If $\varangle A C M=10^{\circ}$ and $\varangle C B M=20^{\circ}$, prove that $A B=M C$.
|
## Solution
Let $O$ be the circumcenter of the triangle $A B C$. Because the triangle $A B C$ is acute, $O$ is in the interior of $\triangle A B C$. Now we have that $\varangle A O C=2 \varangle A B C=160^{\circ}$, so $\varangle A C O=10^{\circ}$ and $\varangle B O C=2 \varangle B A C=140^{\circ}$, so $\varangle C B O=20^{\circ}$. Therefore $O \equiv M$, thus $M A=$ $M B=M C$. Because $\varangle A B O=80^{\circ}-20^{\circ}=60^{\circ}$, the triangle $A B M$ is equilateral and so $A B=M B=M C$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 50 |
G4 Let $S$ be a point inside $\varangle p O q$, and let $k$ be a circle which contains $S$ and touches the legs $O p$ and $O q$ in points $P$ and $Q$ respectively. Straight line $s$ parallel to $O p$ from $S$ intersects $O q$ in a point $R$. Let $T$ be the point of intersection of the ray $(P S$ and circumscribed circle of $\triangle S Q R$ and $T \neq S$. Prove that $O T \| S Q$ and $O T$ is a tangent of the circumscribed circle of $\triangle S Q R$.
|
## Solution
Let $\varangle O P S=\varphi_{1}$ and $\varangle O Q S=\varphi_{2}$. We have that $\varangle O P S=\varangle P Q S=\varphi_{1}$ and $\varangle O Q S=$ $\varangle Q P S=\varphi_{2}$ (tangents to circle $k$ ).
Because $R S \| O P$ we have $\varangle O P S=\varangle R S T=\varphi_{1}$ and $\varangle R Q T=\varangle R S T=\varphi_{1}$ (cyclic quadrilateral $R S Q T$ ). So, we have as follows $\varangle O P T=\varphi_{1}=\varangle R Q T=\varangle O Q T$, which implies that the quadrilateral $O P Q T$ is cyclic. From that we directly obtain $\varangle Q O T=$ $\varangle Q P T=\varphi_{2}=\varangle O Q S$, so $O T \| S Q$. From the cyclic quadrilateral $O P Q T$ by easy calculation we get
$$
\varangle O T R=\varangle O T P-\varangle R T S=\varangle O Q P-\varangle R Q S=\left(\varphi_{1}+\varphi_{2}\right)-\varphi_{2}=\varphi_{1}=\varangle R Q T
$$
Thus, $O T$ is a tangent to the circumscribed circle of $\triangle S Q R$.
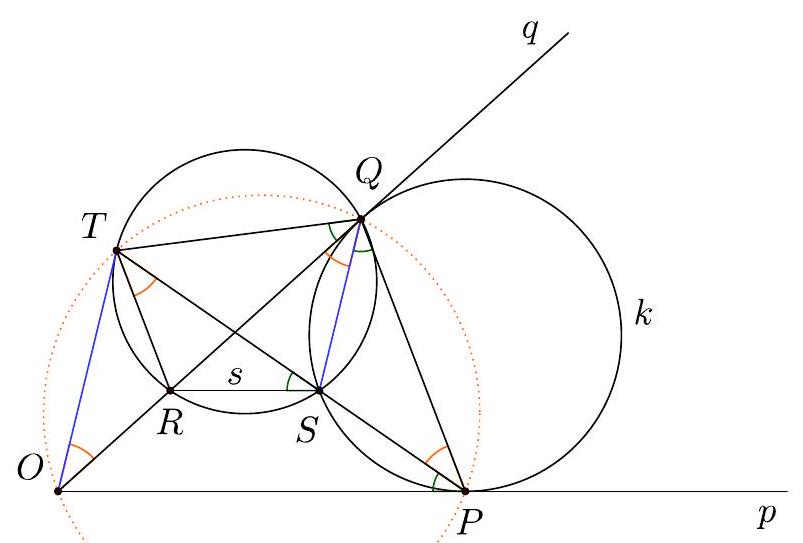
### 2.4 Number Theory
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 51 |
NT2 Prove that the equation $x^{2006}-4 y^{2006}-2006=4 y^{2007}+2007 y$ has no solution in the set of the positive integers.
|
## Solution
We assume the contrary is true. So there are $x$ and $y$ that satisfy the equation. Hence we have
$$
\begin{gathered}
x^{2006}=4 y^{2007}+4 y^{2006}+2007 y+2006 \\
x^{2006}+1=4 y^{2006}(y+1)+2007(y+1) \\
x^{2006}+1=\left(4 y^{2006}+2007\right)(y+1)
\end{gathered}
$$
But $4 y^{2006}+2007 \equiv 3(\bmod 4)$, so $x^{2006}+1$ will have at least one prime divisor of the type $4 k+3$. It is known (and easily obtainable by using Fermat's Little Theorem) that this is impossible.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 52 |
NT3 Let $n>1$ be a positive integer and $p$ a prime number such that $n \mid(p-1)$ and $p \mid\left(n^{6}-1\right)$. Prove that at least one of the numbers $p-n$ and $p+n$ is a perfect square.
|
## Solution
Since $n \mid p-1$, then $p=1+n a$, where $a \geq 1$ is an integer. From the condition $p \mid n^{6}-1$, it follows that $p|n-1, p| n+1, p \mid n^{2}+n+1$ or $p \mid n^{2}-n+1$.
- Let $p \mid n-1$. Then $n \geq p+1>n$ which is impossible.
- Let $p \mid n+1$. Then $n+1 \geq p=1+n a$ which is possible only when $a=1$ and $p=n+1$, i.e. $p-n=1=1^{2}$.
- Let $p \mid n^{2}+n+1$, i.e. $n^{2}+n+1=p b$, where $b \geq 1$ is an integer.
The equality $p=1+n a$ implies $n \mid b-1$, from where $b=1+n c, c \geq 0$ is an integer. We have
$$
n^{2}+n+1=p b=(1+n a)(1+n c)=1+(a+c) n+a c n^{2} \text { or } n+1=a c n+a+c
$$
If $a c \geq 1$ then $a+c \geq 2$, which is impossible. If $a c=0$ then $c=0$ and $a=n+1$. Thus we obtain $p=n^{2}+n+1$ from where $p+n=n^{2}+2 n+1=(n+1)^{2}$.
- Let $p \mid n^{2}-n+1$, i.e. $n^{2}-n+1=p b$ and analogously $b=1+n c$. So
$$
n^{2}-n+1=p b=(1+n a)(1+n c)=1+(a+c) n+a c n^{2} \text { or } n-1=a c n+a+c
$$
Similarly, we have $c=0, a=n-1$ and $p=n^{2}-n+1$ from where $p-n=n^{2}-2 n+1=$ $(n-1)^{2}$.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 53 |
NT4 Let $a, b$ be two co-prime positive integers. A number is called good if it can be written in the form $a x+b y$ for non-negative integers $x, y$. Define the function $f: \mathbb{Z} \rightarrow \mathbb{Z}$ as $f(n)=n-n_{a}-n_{b}$, where $s_{t}$ represents the remainder of $s$ upon division by $t$. Show that an integer $n$ is good if and only if the infinite sequence $n, f(n), f(f(n)), \ldots$ contains only non-negative integers.
|
## Solution
If $n$ is good then $n=a x+b y$ also $n_{a}=(b y)_{a}$ and $n_{b}=(a x)_{b}$ so
$$
f(n)=a x-(a x)_{b}+b y-(b y)_{a}=b y^{\prime}+a x^{\prime}
$$
is also good, thus the sequence contains only good numbers which are non-negative.
Now we have to prove that if the sequence contains only non-negative integers then $n$ is good. Because the sequence is non-increasing then the sequence will become constant from some point onwards. But $f(k)=k$ implies that $k$ is a multiple of $a b$ thus some term of the sequence is good. We are done if we prove the following:
Lemma: $f(n)$ is good implies $n$ is good.
Proof of Lemma: $n=2 n-n_{a}-n_{b}-f(n)=a x^{\prime}+b y^{\prime}-a x-b y=a\left(x^{\prime}-x\right)+b\left(y^{\prime}-y\right)$ and $x^{\prime} \geq x$ because $n \geq f(n) \Rightarrow n-n_{a} \geq f(n)-f(n)_{a} \Rightarrow a x^{\prime} \geq a x+b y-(b y)_{a} \geq a x$. Similarly $y^{\prime} \geq y$.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 54 |
NT5 Let $p$ be a prime number. Show that $7 p+3^{p}-4$ is not a perfect square.
|
## Solution
Assume that for a prime number $p$ greater than $3, m=7 p+3^{p}-4$ is a perfect square. Let $m=n^{2}$ for some $n \in \mathbb{Z}$. By Fermat's Little Theorem,
$$
m=7 p+3^{p}-4 \equiv 3-4 \equiv-1 \quad(\bmod p)
$$
If $p=4 k+3, k \in \mathbb{Z}$, then again by Fermat's Little Theorem
$$
-1 \equiv m^{2 k+1} \equiv n^{4 k+2} \equiv n^{p-1} \equiv 1 \quad(\bmod p), \text { but } p>3
$$
a contradiction. So $p \equiv 1(\bmod 4)$.
Therefore $m=7 p+3^{p}-4 \equiv 3-1 \equiv 2(\bmod 4)$. But this is a contradiction since 2 is not perfect square in $(\bmod 4)$. For $p=2$ we have $m=19$ and for $p=3$ we have $m=44$.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 55 |
## A3
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that:
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq 3(a+b+c+1)
$$
When does equality hold?
|
Solution1. By using AM-GM $\left(x^{2}+y^{2}+z^{2} \geq x y+y z+z x\right)$ we have
$$
\begin{aligned}
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} & \geq\left(a+\frac{1}{b}\right)\left(b+\frac{1}{c}\right)+\left(b+\frac{1}{c}\right)\left(c+\frac{1}{a}\right)+\left(c+\frac{1}{a}\right)\left(a+\frac{1}{b}\right) \\
& =\left(a b+1+\frac{a}{c}+a\right)+\left(b c+1+\frac{b}{a}+b\right)+\left(c a+1+\frac{c}{b}+c\right) \\
& =a b+b c+c a+\frac{a}{c}+\frac{c}{b}+\frac{b}{a}+3+a+b+c
\end{aligned}
$$
Notice that by AM-GM we have $a b+\frac{b}{a} \geq 2 b, b c+\frac{c}{b} \geq 2 c$, and $c a+\frac{a}{c} \geq 2 a$.
Thus,
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq\left(a b+\frac{b}{a}\right)+\left(b c+\frac{c}{b}\right)+\left(c a+\frac{a}{c}\right)+3+a+b+c \geq 3(a+b+c+1)
$$
The equality holds if and only if $a=b=c=1$.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 57 |
## A4
Let $a, b, c$ be positive real numbers such that $a+b+c=1$. Prove that
$$
\frac{7+2 b}{1+a}+\frac{7+2 c}{1+b}+\frac{7+2 a}{1+c} \geq \frac{69}{4}
$$
When does equality hold?
|
Solution1. The inequality can be written as: $\frac{5+2(1+b)}{1+a}+\frac{5+2(1+c)}{1+b}+\frac{5+2(1+a)}{1+c} \geq \frac{69}{4}$.
We substitute $1+a=x, 1+b=y, 1+c=z$.
So, we have to prove the inequality
$$
\frac{5+2 y}{x}+\frac{5+2 z}{y}+\frac{5+2 x}{z} \geq \frac{69}{4} \Leftrightarrow 5\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)+2\left(\frac{y}{x}+\frac{z}{y}+\frac{x}{z}\right) \geq \frac{69}{4}
$$
where $x, y, z>1$ real numbers and $x+y+z=4$.
We have
- $\frac{x+y+z}{3} \geq \frac{3}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}} \Leftrightarrow \frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq \frac{9}{x+y+z} \Leftrightarrow \frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq \frac{9}{4}$
- $\frac{y}{x}+\frac{z}{y}+\frac{x}{z} \geq 3 \cdot \sqrt[3]{\frac{y}{x} \cdot \frac{z}{y} \cdot \frac{x}{z}}=3$
Thus, $\frac{5+2 y}{x}+\frac{5+2 z}{y}+\frac{5+2 x}{z}=5\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)+2\left(\frac{y}{x}+\frac{z}{y}+\frac{x}{z}\right) \geq 5 \cdot \frac{9}{4}+2 \cdot 3=\frac{69}{4}$.
The equality holds, when $\left(x=y=z, \frac{y}{x}=\frac{z}{y}=\frac{x}{z}, x+y+z=4\right)$, thus $x=y=z=\frac{4}{3}$, i.e. $a=b=c=\frac{1}{3}$.
## (Egw)
人s
Let $x, y, z$ be non-negative real numbers satisfying $x+y+z=x y z$. Prove that
$$
2\left(x^{2}+y^{2}+z^{2}\right) \geq 3(x+y+z)
$$
and determine when equality occurs.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 58 |
## A6
Let $a, b, c$ be positive real numbers. Prove that
$$
\left(\left(3 a^{2}+1\right)^{2}+2\left(1+\frac{3}{b}\right)^{2}\right)\left(\left(3 b^{2}+1\right)^{2}+2\left(1+\frac{3}{c}\right)^{2}\right)\left(\left(3 c^{2}+1\right)^{2}+2\left(1+\frac{3}{a}\right)^{2}\right) \geq 48^{3}
$$
When does equality hold?
|
Solution. Let $x$ be a positive real number. By AM-GM we have $\frac{1+x+x+x}{4} \geq x^{\frac{3}{4}}$, or equivalently $1+3 x \geq 4 x^{\frac{3}{4}}$. Using this inequality we obtain:
$$
\left(3 a^{2}+1\right)^{2} \geq 16 a^{3} \text { and } 2\left(1+\frac{3}{b}\right)^{2} \geq 32 b^{-\frac{3}{2}}
$$
Moreover, by inequality of arithmetic and geometric means we have
$$
f(a, b)=\left(3 a^{2}+1\right)^{2}+2\left(1+\frac{3}{b}\right)^{2} \geq 16 a^{3}+32 b^{-\frac{3}{2}}=16\left(a^{3}+b^{-\frac{3}{2}}+b^{-\frac{3}{2}}\right) \geq 48 \frac{a}{b}
$$
Therefore, we obtain
$$
f(a, b) f(b, c) f(c, a) \geq 48 \cdot \frac{a}{b} \cdot 48 \cdot \frac{b}{c} \cdot 48 \cdot \frac{c}{a}=48^{3}
$$
Equality holds only when $a=b=c=1$.
## 1 IH $^{\text {th J.M. }} 2014$
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 59 |
## A8
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove the inequality
$$
\frac{1}{x(a y+b)}+\frac{1}{y(a z+b)}+\frac{1}{z(a x+b)} \geq 3 \text {, if: }
$$
a) $a=0$ and $b=1$;
b) $a=1$ and $b=0$;
c) $a+b=1$ for $a, b>0$
When does the equality hold true?
|
Solution. a) The inequality reduces to $\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq 3$, which follows directly from the AM-GM inequality.
Equality holds only when $x=y=z=1$.
b) Here the inequality reduces to $\frac{1}{x y}+\frac{1}{y z}+\frac{1}{z x} \geq 3$, i.e. $x+y+z \geq 3$, which also follows from the AM-GM inequality.
Equality holds only when $x=y=z=1$.
c) Let $m, n$ and $p$ be such that $x=\frac{m}{n}, y=\frac{n}{p}$ и $z=\frac{p}{m}$. The inequality reduces to
$$
\frac{n p}{a m n+b m p}+\frac{p m}{a n p+b n m}+\frac{m n}{a p m+b p n} \geq 3
$$
By substituting $u=n p, v=p m$ and $w=m n$, (1) becomes
$$
\frac{u}{a w+b v}+\frac{v}{a u+b w}+\frac{w}{a v+b u} \geq 3
$$
The last inequality is equivalent to
$$
\frac{u^{2}}{a u w+b u v}+\frac{v^{2}}{a u v+b v w}+\frac{w^{2}}{a v w+b u w} \geq 3
$$
Cauchy-Schwarz Inequality implies
$$
\frac{u^{2}}{a u w+b u v}+\frac{v^{2}}{a u v+b v w}+\frac{w^{2}}{a v w+b u w} \geq \frac{(u+v+w)^{2}}{a u w+b u v+a u v+b v w+a v w+b u w}=\frac{(u+v+w)^{2}}{u w+v u+w v}
$$
Thus, the problem simplifies to $(u+v+w)^{2} \geq 3(u w+v u+w v)$, which is equivalent to $(u-v)^{2}+(v-w)^{2}+(w-u)^{2} \geq 0$.
Equality holds only when $u=v=w$, that is only for $x=y=z=1$.
Remark. The problem can be reformulated:
Let $a, b, x, y$ and $z$ be nonnegative real numbers such that $x y z=1$ and $a+b=1$. Prove the inequality
$$
\frac{1}{x(a y+b)}+\frac{1}{y(a z+b)}+\frac{1}{z(a x+b)} \geq 3
$$
When does the equality hold true?
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 60 |
## A9
Let $n$ be a positive integer, and let $x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{n}$ be positive real numbers such that $x_{1}+\ldots+x_{n}=y_{1}+\ldots+y_{n}=1$. Show that
$$
\left|x_{1}-y_{1}\right|+\ldots\left|x_{n}-y_{n}\right| \leq 2-\min _{1 \leq i \leq n} \frac{x_{i}}{y_{i}}-\min _{1 \leq i \leq n} \frac{y_{i}}{x_{i}}
$$
|
Solution. Up to reordering the real numbers $x_{i}$ and $y_{i}$, we may assume that $\frac{x_{1}}{y_{1}} \leq \ldots \leq \frac{x_{n}}{y_{n}}$. Let $A=\frac{x_{1}}{y_{1}}$ and $B=\frac{x_{n}}{y_{n}}$, and $\mathrm{S}=\left|x_{1}-y_{1}\right|+\ldots\left|x_{n}-y_{n}\right|$. Our aim is to prove that $S \leq 2-A-\frac{1}{B}$.
First, note that we cannot have $A>1$, since that would imply $x_{i}>y_{i}$ for all $i \leq n$, hence $x_{1}+\ldots+x_{n}>y_{1}+\ldots+y_{n}$. Similarly, we cannot have $B<1$, since that would imply $x_{i}<y_{i}$ for all $i \leq n$, hence $x_{1}+\ldots+x_{n}<y_{1}+\ldots+y_{n}$.
If $n=1$, then $x_{1}=y_{1}=A=B=1$ and $S=0$, hence $S \leq 2-A-\frac{1}{B}$. For $n \geq 2$ let $1 \leq k<n$ be some integer such that $\frac{x_{k}}{y_{k}} \leq 1 \leq \frac{x_{k+1}}{y_{k+1}}$. We define the positive real numbers $X_{1}=x_{1}+\ldots+x_{k}$, $X_{2}=x_{k+1}+\ldots+x_{n}, Y_{1}=y_{1}+\ldots+y_{k}, Y_{2}=y_{k+1}+\ldots+y_{n}$. Note that $Y_{1} \geq X_{1} \geq A Y_{1}$ and $Y_{2} \leq X_{2} \leq B Y_{2}$. Thus, $A \leq \frac{X_{1}}{Y_{1}} \leq 1 \leq \frac{X_{2}}{Y_{2}} \leq B$. In addition, $S=Y_{1}-X_{1}+X_{2}-Y_{2}$.
From $0<X_{2}, Y_{1} \leq 1,0 \leq Y_{1}-X_{1}$ and $0 \leq X_{2}-Y_{2}$, follows
$$
S=Y_{1}-X_{1}+X_{2}-Y_{2}=\frac{Y_{1}-X_{1}}{Y_{1}}+\frac{X_{2}-Y_{2}}{X_{2}}=2-\frac{X_{1}}{Y_{1}}-\frac{Y_{2}}{X_{2}} \leq 2-A-\frac{1}{B}
$$
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 61 |
## C1
Several (at least two) segments are drawn on a board. Select two of them, and let $a$ and $b$ be their lengths. Delete the selected segments and draw a segment of length $\frac{a b}{a+b}$. Continue this procedure until only one segment remains on the board. Prove:
a) the length of the last remaining segment does not depend on the order of the deletions.
b) for every positive integer $n$, the initial segments on the board can be chosen with distinct integer lengths, such that the last remaining segment has length $n$.
|
Solution. a) Observe that $\frac{1}{\frac{a b}{a+b}}=\frac{1}{a}+\frac{1}{b}$. Thus, if the lengths of the initial segments on the board were $a_{1}, a_{2}, \ldots, a_{n}$, and $c$ is the length of the last remaining segment, then $\frac{1}{c}=\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{n}}$ , proving a).
b) From a) and the equation $\frac{1}{n}=\frac{1}{2 n}+\frac{1}{3 n}+\frac{1}{6 n}$ it follows that if the lengths of the starting segments are $2 n, 3 n$ and $6 n$, then the length of the last remaining segment is $n$.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 62 |
## G2
Let $A B C$ be an acute triangle with $\overline{A B}<\overline{A C}<\overline{B C}$ and $c(O, R)$ be its circumcircle. Denote with $D$ and $E$ be the points diametrically opposite to the points $B$ and $C$, respectively. The circle $c_{1}(A, \overline{A E})$ intersects $\overline{A C}$ at point $K$, the circle $c_{2}(A, \overline{A D})$ intersects $B A$ at point $L(A$ lies between $B$ and $L$ ). Prove that the lines $E K$ and $D L$ meet on the circle $c$.
|
Solution. Let $\mathrm{M}$ be the point of intersection of the line $D L$ with the circle $c(O, R)$ (we choose $M \equiv D$ if $L D$ is tangent to $c$ and $M$ to be the second intersecting point otherwise). It is
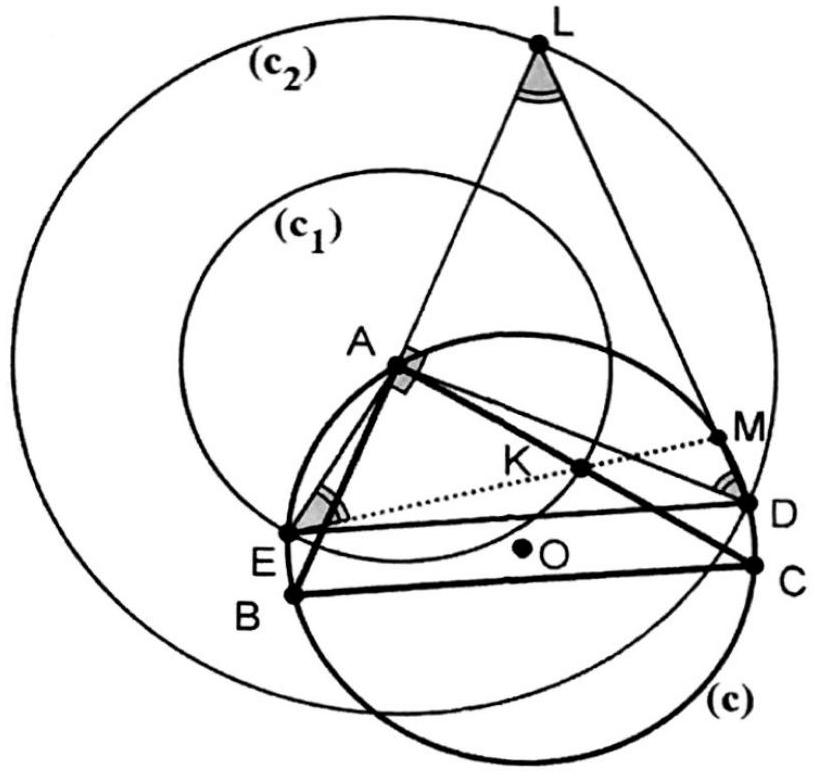
sufficient to prove that the points $E, K$ and $M$ are collinear.
We have that $\measuredangle E A C=90^{\circ}$ (since $E C$ is diameter of the circle $c$ ). The triangle $A E K$ is right-angled and isosceles ( $\overline{A E}$ and $\overline{A K}$ are radii of the circle $c_{1}$ ). Therefore
$$
\measuredangle \mathrm{AEK}=\measuredangle \mathrm{AKE}=45^{\circ} \text {. }
$$
Similarly, we obtain that $\measuredangle B A D=90^{\circ}=\measuredangle D A L$. Since $\overline{A D}=\overline{A L}$ the triangle $A D L$ is right-angled and isosceles, we have
$$
\measuredangle \mathrm{ADL}=\measuredangle \mathrm{A} L D=45^{\circ} .
$$
If $M$ is between $D$ and $L$, then $\measuredangle \mathrm{ADM}=\measuredangle A E M$, because they are inscribed in the circle $c(O, R)$ and they correspond to the same arch $\overparen{A M}$. Hence $\measuredangle \mathrm{AEK}=\measuredangle \mathrm{AEM}=45^{\circ}$ i.e. the points $E, K, M$ are collinear.
If $D$ is between $M$ and $L$, then $\measuredangle \mathrm{ADM}+\measuredangle A E M=180^{\circ}$ as opposite angles in cyclic quadrilateral. Hence $\measuredangle \mathrm{AEK}=\measuredangle \mathrm{AEM}=45^{\circ}$ i.e. the points $E, K, M$ are collinear.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 63 |
## G4
Let $A B C$ be a triangle such that $\overline{A B} \neq \overline{A C}$. Let $M$ be a midpoint of $\overline{B C}, H$ the orthocenter of $A B C, O_{1}$ the midpoint of $\overline{A H}$ and $O_{2}$ the circumcenter of $B C H$. Prove that $O_{1} A M O_{2}$ is a parallelogram.
|
Solution1. Let $O_{2}^{\prime}$ be the point such that $O_{1} A M O_{2}^{\prime}$ is a parallelogram. Note that $\overrightarrow{M O_{2}}=\overrightarrow{A O_{1}}=\overrightarrow{O_{1} H}$. Therefore, $O_{1} H O_{2}^{\prime} M$ is a parallelogram and $\overrightarrow{M O_{1}}=\overrightarrow{O_{2} H}$.
Since $M$ is the midpoint of $\overline{B C}$ and $O_{1}$ is the midpoint of $\overline{A H}$, it follows that $4 \overrightarrow{M O_{1}}=\overrightarrow{B A}+\overrightarrow{B H}+\overrightarrow{C A}+\overrightarrow{C H}=2(\overrightarrow{C A}+\overrightarrow{B H})$. Moreover, let $B^{\prime}$ be the midpoint of $\overrightarrow{B H}$. Then,
$$
\begin{aligned}
2 \overrightarrow{O_{2}^{\prime B}} \cdot \overrightarrow{B H} & =\left(\overline{O_{2}^{\prime H}}+\overline{O_{2}^{\prime B}}\right) \cdot \overrightarrow{B H}=\left(2 \overline{O_{2}^{\prime} H}+\overrightarrow{H B}\right) \cdot \overrightarrow{B H}= \\
& =\left(2 \overline{M O_{1}}+\overline{H B}\right) \cdot \overline{B H}=(\overline{C A}+\overrightarrow{B H}+\overrightarrow{H B}) \cdot \overrightarrow{B H}=\overline{C A} \cdot \overrightarrow{B H}=0 .
\end{aligned}
$$
By $\vec{a} \cdot \vec{b}$ we denote the inner product of the vectors $\vec{a}$ and $\vec{b}$.
Therefore, $O_{2}^{\prime}$ lies on the perpendicular bisector of $\overline{B H}$. Since $B$ and $C$ play symmetric roles, $\mathrm{O}_{2}^{\prime}$ also lies on the perpendicular bisector of $\overline{\mathrm{CH}}$, hence $\mathrm{O}_{2}^{\prime}$ is the circumcenter of $\triangle B C H$ and $\mathrm{O}_{2}=\mathrm{O}_{2}^{\prime}$.
Note: The condition $\overline{A B} \neq \overline{A C}$ just aims at ensuring that the parallelogram $O_{1} A N O_{2}$ is not degenerate, hence at helping students to focus on the "general" case.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 64 |
## G5
Let $A B C$ be a triangle with $\overline{A B} \neq \overline{B C}$, and let $B D$ be the internal bisector of $\measuredangle A B C(D \in A C)$. Denote the midpoint of the arc $A C$ which contains point BbyM. The circumcircle of the triangle $B D M$ intersects the segment $A B$ at point $K \neq B$, and let $J$ be the reflection of $A$ with respect to $K$. If $D J \cap A M=\{O\}$, prove that the points $J, B, M, O$ belong to the same circle.
|
## Solution1.
Let the circumcircle of the triangle $B D M$ intersect the line segment $B C$ at point $L \neq B$. From $\measuredangle C B D=\measuredangle D B A$ we have $\overline{D L}=\overline{D K}$. Since $\measuredangle L C M=\measuredangle B C M=\measuredangle B A M=\measuredangle K A M, \overline{M C}=\overline{M A}$ and
$$
\measuredangle L M C=\measuredangle L M K-\measuredangle C M K=\measuredangle L B K-\measuredangle C M K=\measuredangle C B A-\measuredangle C M K=\measuredangle C M A-\measuredangle C M K=\measuredangle K M A,
$$
it follows that triangles $M L C$ and $M K A$ are congruent, which implies $\overline{C L}=\overline{A K}=\overline{K J}$. Furthermore, $\measuredangle C L D=180^{\circ}-\measuredangle B L D=\measuredangle D K B=\measuredangle D K J$ and $\overline{D L}=\overline{D K}$, it follows that triangles $D C L$ and $D J K$ are congruent. Hence, $\angle D C L=\angle D J K=\measuredangle B J O$. Then
$$
\measuredangle B J O+\measuredangle B M O=\angle D C L+\angle B M A=\angle B C A+180^{\circ}-\angle B C A=180^{\circ}
$$
so the points $J, B, M, O$ belong to the same circle, q.e.d.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 65 |
## G6
Let $A B C D$ be a quadrilateral whose sides $A B$ and $C D$ are not parallel, and let $O$ be the intersection of its diagonals. Denote with $H_{1}$ and $H_{2}$ the orthocenters of the triangles $O A B$ and OCD, respectively. If $M$ and $N$ are the midpoints of the segments $\overline{A B}$ and $\overline{C D}$, respectively, prove that the lines $M N$ and $\mathrm{H}_{1} \mathrm{H}_{2}$ are parallel if and only if $\overline{A C}=\overline{B D}$.
|
## Solution.
Let $A^{\prime}$ and $B^{\prime}$ be the feet of the altitudes drawn from $A$ and $B$ respectively in the triangle $A O B$, and $C^{\prime}$ and $D^{\prime}$ are the feet of the altitudes drawn from $C$ and $D$ in the triangle $C O D$. Obviously, $A^{\prime}$ and $D^{\prime}$ belong to the circle $c_{1}$ of diameter $\overline{A D}$, while $B^{\prime}$ and $C^{\prime}$ belong to the circle $c_{2}$ of diameter $\overline{B C}$.
It is easy to see that triangles $H_{1} A B$ and $H_{1} B^{\prime} A^{\prime}$ are similar. It follows that $\overline{H_{1} A} \cdot \overline{H_{1} A^{\prime}}=\overline{H_{1} B} \cdot \overline{H_{1} B^{\prime}}$. (Alternatively, one could notice that the quadrilateral $A B A^{\prime} B^{\prime}$ is cyclic and obtain the previous relation by writing the power of $H_{1}$ with respect to its circumcircle.) It
follows that $H_{1}$ has the same power with respect to circles $c_{1}$ and $c_{2}$. Thus, $H_{1}$ (and similarly, $\mathrm{H}_{2}$ ) is on the radical axis of the two circles.
The radical axis being perpendicular to the line joining the centers of the two circles, one concludes that $\mathrm{H}_{1} \mathrm{H}_{2}$ is perpendicular to $P Q$, where $P$ and $Q$ are the midpoints of the sides $\overline{A D}$ and $\overline{B C}$, respectively. ( $P$ and $Q$ are the centers of circles $c_{1}$ and $c_{2}$.)
The condition $H_{1} H_{2} \| M N$ is equivalent to $M N \perp P Q$. As $M P N Q$ is a parallelogram, we conclude that $H_{1} H_{2} \| M N \Leftrightarrow M N \perp P Q \Leftrightarrow M P N Q$ a rhombus $\Leftrightarrow \overline{M P}=\overline{M Q} \Leftrightarrow \overline{A C}=\overline{B D}$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 66 |
N4
Prove there are no integers $a$ and $b$ satisfying the following conditions:
i) $16 a-9 b$ is a prime number
ii) $\quad a b$ is a perfect square
iii) $a+b$ is a perfect square
|
Solution. Suppose $a$ and $b$ be integers satisfying the given conditions. Let $p$ be a prime number, $n$ and $m$ be integers. Then we can write the conditions as follows:
$$
\begin{aligned}
& 16 a-9 b=p \\
& a b=n^{2} \\
& a+b=m^{2}
\end{aligned}
$$
Moreover, let $d=g d c(a, b)$ and $a=d x, b=d y$ for some relatively prime integers $x$ and $y$. Obviously $a \neq 0$ and $b \neq 0, a$ and $b$ are positive (by (2) and (3)).
From (2) follows that $x$ and $y$ are perfect squares, say $x=l^{2}$ and $y=s^{2}$.
From (1), $d \mid p$ and hence $d=p$ or $d=1$. If $d=p$, then $16 x-9 y=1$, and we obtain $x=9 k+4$, $y=16 k+7$ for some nonnegative integer $k$. But then $s^{2}=y \equiv 3(\bmod 4)$, which is a contradiction.
If $d=1$ then $16 l^{2}-9 s^{2}=p \Rightarrow(4 l-3 s)(4 l+3 s)=p \Rightarrow(4 l+3 s=p \wedge 4 l-3 s=1)$.
By adding the last two equations we get $8 l=p+1$ and by subtracting them we get $6 s=p-1$. Therefore $p=24 t+7$ for some integer $t$ and $a=(3 t+1)^{2}$ and $b=(4 t+1)^{2}$ satisfy the conditions (1) and (2). By (3) we have $m^{2}=(3 t+1)^{2}+(4 t+1)^{2}=25 t^{2}+14 t+2$, or equivalently $25 m^{2}=(25 t+7)^{2}+1$.
Since the difference between two nonzero perfect square cannot be 1 , we have a contradiction. As a result there is no solution.
## NS
Find all nonnegative integers $x, y, z$ such that
$$
2013^{x}+2014^{y}=2015^{z}
$$
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 67 |
A2. Let $a, b, c$ be positive real numbers such that $a b c=\frac{2}{3}$. Prove that
$$
\frac{a b}{a+b}+\frac{b c}{b+c}+\frac{c a}{c+a} \geqslant \frac{a+b+c}{a^{3}+b^{3}+c^{3}}
$$
|
Solution. The given inequality is equivalent to
$$
\left(a^{3}+b^{3}+c^{3}\right)\left(\frac{a b}{a+b}+\frac{b c}{b+c}+\frac{c a}{c+a}\right) \geqslant a+b+c
$$
By the AM-GM Inequality it follows that
$$
a^{3}+b^{3}=\frac{a^{3}+a^{3}+b^{3}}{3}+\frac{b^{3}+b^{3}+a^{3}}{3} \geqslant a^{2} b+b^{2} a=a b(a+b)
$$
Similarly we have
$$
b^{3}+c^{3} \geqslant b c(b+c) \quad \text { and } \quad c^{3}+a^{3} \geqslant c a(c+a)
$$
Summing the three inequalities we get
$$
2\left(a^{3}+b^{2}+c^{3}\right) \geqslant(a b(a+b)+b c(b+c)+c a(c+a))
$$
From the Cauchy-Schwarz Inequality we have
$$
(a b(a+b)+b c(b+c)+c a(c+a))\left(\frac{a b}{a+b}+\frac{b c}{b+c}+\frac{c a}{c+a}\right) \geqslant(a b+b c+c a)^{2}
$$
We also have
$$
(a b+b c+c a)^{2} \geqslant 3(a b \cdot b c+b c \cdot c a+c a \cdot a b)=3 a b c(a+b+c)=2(a+b+c)
$$
Combining together (2),(3) and (4) we obtain (1) which is the required inequality.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 69 |
A4. Let $a, b$ be two distinct real numbers and let $c$ be a positive real number such that
$$
a^{4}-2019 a=b^{4}-2019 b=c
$$
Prove that $-\sqrt{c}<a b<0$.
|
Solution. Firstly, we see that
$$
2019(a-b)=a^{4}-b^{4}=(a-b)(a+b)\left(a^{2}+b^{2}\right)
$$
Since $a \neq b$, we get $(a+b)\left(a^{2}+b^{2}\right)=2019$, so $a+b \neq 0$. Thus
$$
\begin{aligned}
2 c & =a^{4}-2019 a+b^{4}-2019 b \\
& =a^{4}+b^{4}-2019(a+b) \\
& =a^{4}+b^{4}-(a+b)^{2}\left(a^{2}+b^{2}\right) \\
& =-2 a b\left(a^{2}+a b+b^{2}\right)
\end{aligned}
$$
Hence $a b\left(a^{2}+a b+b^{2}\right)=-c-a b$ (the equality does not occur since $a+b \neq 0)$. So
$$
-c=a b\left(a^{2}+a b+b^{2}\right)<-(a b)^{2} \Longrightarrow(a b)^{2}<c \Rightarrow-\sqrt{c}<a b<\sqrt{c}
$$
Therefore, we have $-\sqrt{c}<a b<0$.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 70 |
A5. Let $a, b, c, d$ be positive real numbers such that $a b c d=1$. Prove the inequality
$$
\frac{1}{a^{3}+b+c+d}+\frac{1}{a+b^{3}+c+d}+\frac{1}{a+b+c^{3}+d}+\frac{1}{a+b+c+d^{3}} \leqslant \frac{a+b+c+d}{4}
$$
|
Solution. From the Cauchy-Schwarz Inequality, we obtain
$$
(a+b+c+d)^{2} \leqslant\left(a^{3}+b+c+d\right)\left(\frac{1}{a}+b+c+d\right)
$$
Using this, together with the other three analogous inequalities, we get
$$
\begin{aligned}
\frac{1}{a^{3}+b+c+d}+\frac{1}{a+b^{3}+c+d}+\frac{1}{a+b+c^{3}+d} & +\frac{1}{a+b+c+d^{3}} \\
& \leqslant \frac{3(a+b+c+d)+\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}\right)}{(a+b+c+d)^{2}}
\end{aligned}
$$
So it suffices to prove that
$$
(a+b+c+d)^{3} \geqslant 12(a+b+c+d)+4\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}\right)
$$
or equivalently, that
$$
\begin{aligned}
& \left(a^{3}+b^{3}+c^{3}+d^{3}\right)+3 \sum a^{2} b+6(a b c+a b d+a c d+b c d) \\
& \quad \geqslant 12(a+b+c+d)+4(a b c+a b d+a c d+b c d)
\end{aligned}
$$
(Here, the sum is over all possible $x^{2} y$ with $x, y \in\{a, b, c, d\}$ and $x \neq y$.) From the AM-GM Inequality we have
$a^{3}+a^{2} b+a^{2} b+a^{2} c+a^{2} c+a^{2} d+a^{2} d+b^{2} a+c^{2} a+d^{2} a+b c d+b c d \geqslant 12 \sqrt[12]{a^{18} b^{6} c^{6} d^{6}}=12 a$.
Similarly, we get three more inequalities. Adding them together gives the inequality we wanted. Equality holds if and only if $a=b=c=d=1$.
Remark by PSC. Alternatively, we can finish off the proof by using the following two inequalities: Firstly, we have $a+b+c+d \geqslant 4 \sqrt[4]{a b c d}=4$ by the AM-GM Inequality, giving
$$
\frac{3}{4}(a+b+c+d)^{3} \geqslant 12(a+b+c+d)
$$
Secondly, by Mclaurin's Inequality, we have
$$
\left(\frac{a+b+c+d}{4}\right)^{3} \geqslant \frac{b c d+a c d+a b d+a b c}{4}
$$
giving
$$
\frac{1}{4}(a+b+c+d)^{3} \geqslant 4(b c d+a c d+a b d+a b c)
$$
Adding those inequlities we get the required result.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 71 |
A6. Let $a, b, c$ be positive real numbers. Prove the inequality
$$
\left(a^{2}+a c+c^{2}\right)\left(\frac{1}{a+b+c}+\frac{1}{a+c}\right)+b^{2}\left(\frac{1}{b+c}+\frac{1}{a+b}\right)>a+b+c
$$
|
Solution. By the Cauchy-Schwarz Inequality, we have
$$
\frac{1}{a+b+c}+\frac{1}{a+c} \geqslant \frac{4}{2 a+b+2 c}
$$
and
$$
\frac{1}{b+c}+\frac{1}{a+b} \geqslant \frac{4}{a+2 b+c}
$$
Since
$$
a^{2}+a c+c^{2}=\frac{3}{4}(a+c)^{2}+\frac{1}{4}(a-c)^{2} \geqslant \frac{3}{4}(a+c)^{2}
$$
then, writing $L$ for the Left Hand Side of the required inequality, we get
$$
L \geqslant \frac{3(a+c)^{2}}{2 a+b+2 c}+\frac{4 b^{2}}{a+2 b+c}
$$
Using again the Cauchy-Schwarz Inequality, we have:
$$
L \geqslant \frac{(\sqrt{3}(a+c)+2 b)^{2}}{3 a+3 b+3 c}>\frac{(\sqrt{3}(a+c)+\sqrt{3} b)^{2}}{3 a+3 b+3 c}=a+b+c
$$
Alternative Question by Proposers. Let $a, b, c$ be positive real numbers. Prove the inequality
$$
\frac{a^{2}}{a+c}+\frac{b^{2}}{b+c}>\frac{a b-c^{2}}{a+b+c}+\frac{a b}{a+b}
$$
Note that both this inequality and the original one are equivalent to
$$
\left(c+\frac{a^{2}}{a+c}\right)+\left(a-\frac{a b-c^{2}}{a+b+c}\right)+\frac{b^{2}}{b+c}+\left(b-\frac{a b}{a+b}\right)>a+b+c
$$
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 72 |
A7. Show that for any positive real numbers $a, b, c$ such that $a+b+c=a b+b c+c a$, the following inequality holds
$$
3+\sqrt[3]{\frac{a^{3}+1}{2}}+\sqrt[3]{\frac{b^{3}+1}{2}}+\sqrt[3]{\frac{c^{3}+1}{2}} \leqslant 2(a+b+c)
$$
|
Solution. Using the condition we have
$$
a^{2}-a+1=a^{2}-a+1+a b+b c+c a-a-b-c=(c+a-1)(a+b-1)
$$
Hence we have
$$
\sqrt[3]{\frac{a^{3}+1}{2}}=\sqrt[3]{\frac{(a+1)\left(a^{2}-a+1\right)}{2}}=\sqrt[3]{\left(\frac{a+1}{2}\right)(c+a-1)(a+b-1)}
$$
Using the last equality together with the AM-GM Inequality, we have
$$
\begin{aligned}
\sum_{\mathrm{cyc}} \sqrt[3]{\frac{a^{3}+1}{2}} & =\sum_{\mathrm{cyc}} \sqrt[3]{\left(\frac{a+1}{2}\right)(c+a-1)(a+b-1)} \\
& \leqslant \sum_{\mathrm{cyc}} \frac{\frac{a+1}{2}+c+a-1+a+b-1}{3} \\
& =\sum_{c y c} \frac{5 a+2 b+2 c-3}{6} \\
& =\frac{3(a+b+c-1)}{2}
\end{aligned}
$$
Hence it is enough to prove that
$$
3+\frac{3(a+b+c-1)}{2} \leqslant 2(a+b+c)
$$
or equivalently, that $a+b+c \geqslant 3$. From a well- known inequality and the condition, we have
$$
(a+b+c)^{2} \geqslant 3(a b+b c+c a)=3(a+b+c)
$$
thus $a+b+c \geqslant 3$ as desired.
Alternative Proof by PSC. Since $f(x)=\sqrt[3]{x}$ is concave for $x \geqslant 0$, by Jensen's Inequality we have
$$
\sqrt[3]{\frac{a^{3}+1}{2}}+\sqrt[3]{\frac{b^{3}+1}{2}}+\sqrt[3]{\frac{c^{3}+1}{2}} \leqslant 3 \sqrt[3]{\frac{a^{3}+b^{3}+c^{3}+3}{6}}
$$
So it is enough to prove that
$$
\sqrt[3]{\frac{a^{3}+b^{3}+c^{3}+3}{6}} \leqslant \frac{2(a+b+c)-3}{3}
$$
We now write $s=a+b+c=a b+b c+c a$ and $p=a b c$. We have
$$
a^{2}+b^{2}+c^{2}=(a+b+c)^{2}-2(a b+b c+c a)=s^{2}-2 s
$$
and
$$
r=a^{2} b+a b^{2}+b^{2} c+b c^{2}+c^{2} a+c a^{2}=(a b+b c+c a)(a+b+c)-3 a b c=s^{2}-3 p
$$
Thus,
$$
a^{3}+b^{3}+c^{3}=(a+b+c)^{3}-3 r-6 a b c=s^{3}-3 s^{2}+3 p
$$
So to prove (1), it is enough to show that
$$
\frac{s^{3}-3 s^{2}+3 p+3}{6} \leqslant \frac{(2 s-3)^{3}}{27}
$$
Expanding, this is equivalent to
$$
7 s^{3}-45 s^{2}+108 s-27 p-81 \geqslant 0
$$
By the AM-GM Inequality we have $s^{3} \geqslant 27 p$. So it is enough to prove that $p(s) \geqslant 0$, where
$$
p(s)=6 s^{3}-45 s^{2}+108 s-81=3(s-3)^{2}(2 s-3)
$$
It is easy to show that $s \geqslant 3$ (e.g. as in the first solution) so $p(s) \geqslant 0$ as required.
## COMBINATORICS
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 73 |
C1. Let $S$ be a set of 100 positive integers having the following property:
"Among every four numbers of $S$, there is a number which divides each of the other three or there is a number which is equal to the sum of the other three."
Prove that the set $S$ contains a number which divides each of the other 99 numbers of $S$.
|
Solution. Let $a<b$ be the two smallest numbers of $S$ and let $d$ be the largest number of $S$. Consider any two other numbers $x<y$ of $S$. For the quadruples $(a, b, x, d)$ and $(a, b, y, d)$ we cannot get both of $d=a+b+x$ and $d=a+b+y$, since $a+b+x<a+b+y$. From here, we get $a \mid b$ and $a \mid d$.
Consider any number $s$ of $S$ different from $a, b, d$. From the condition of the problem, we get $d=a+b+s$ or $a$ divides $b, s$ and $d$. But since we already know that $a$ divides $b$ and $d$ anyway, we also get that $a \mid s$, as in the first case we have $s=d-a-b$. This means that $a$ divides all other numbers of $S$.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 74 |
C2. In a certain city there are $n$ straight streets, such that every two streets intersect, and no three streets pass through the same intersection. The City Council wants to organize the city by designating the main and the side street on every intersection. Prove that this can be done in such way that if one goes along one of the streets, from its beginning to its end, the intersections where this street is the main street, and the ones where it is not, will apear in alternating order.
|
Solution. Pick any street $s$ and organize the intersections along $s$ such that the intersections of the two types alternate, as in the statement of the problem.
On every other street $s_{1}$, exactly one intersection has been organized, namely the one where $s_{1}$ intersects $s$. Call this intersection $I_{1}$. We want to organize the intersections along $s_{1}$ such that they alternate between the two types. Note that, as $I_{1}$ is already organized, we have exactly one way to organize the remaining intersections along $s_{1}$.
For every street $s_{1} \neq s$, we can apply the procedure described above. Now, we only need to show that every intersection not on $s$ is well-organized. More precisely, this means that for every two streets $s_{1}, s_{2} \neq s$ intersecting at $s_{1} \cap s_{2}=A, s_{1}$ is the main street on $A$ if and only if $s_{2}$ is the side street on $A$.
Consider also the intersections $I_{1}=s_{1} \cap s$ and $I_{2}=s_{2} \cap s$. Now, we will define the "role" of the street $t$ at the intersection $X$ as "main" if this street $t$ is the main street on $X$, and "side" otherwise. We will prove that the roles of $s_{1}$ and $s_{2}$ at $A$ are different.
Consider the path $A \rightarrow I_{1} \rightarrow I_{2} \rightarrow A$. Let the number of intersections between $A$ and $I_{1}$ be $u_{1}$, the number of these between $A$ and $I_{2}$ be $u_{2}$, and the number of these between $I_{1}$ and $I_{2}$ be $v$. Now, if we go from $A$ to $I_{1}$, we will change our role $u_{1}+1$ times, as we will encounter $u_{1}+1$ new intersections. Then, we will change our street from $s_{1}$ to $s$, changing our role once more. Then, on the segment $I_{1} \rightarrow I_{2}$, we have $v+1$ new role changes, and after that one more when we change our street from $s_{1}$ to $s_{2}$. The journey from $I_{2}$ to $A$ will induce $u_{2}+1$ new role changes, so in total we have changed our role $u_{1}+1+1+v+1+1+u_{2}+1=u_{1}+v+u_{2}+5$, As we try to show that roles of $s_{1}$ and $s_{2}$ differ, we need to show that the number of role changes is odd, i.e. that $u_{1}+v+u_{2}+5$ is odd.
Obviously, this claim is equivalent to $2 \mid u_{1}+v+u_{2}$. But $u_{1}, v$ and $u_{2}$ count the number of intersections of the triangle $A I_{1} I_{2}$ with streets other than $s, s_{1}, s_{2}$. Since every street other than $s, s_{1}, s_{2}$ intersects the sides of $A I_{1} I_{2}$ in exactly two points, the total number of intersections is even. As a consequence, $2 \mid u_{1}+v+u_{2}$ as required.
|
proof
|
Combinatorics
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 75 |
G1. Let $A B C$ be a right-angled triangle with $\hat{A}=90^{\circ}$ and $\hat{B}=30^{\circ}$. The perpendicular at the midpoint $M$ of $B C$ meets the bisector $B K$ of the angle $\hat{B}$ at the point $E$. The perpendicular bisector of $E K$ meets $A B$ at $D$. Prove that $K D$ is perpendicular to $D E$.
|
Solution. Let $I$ be the incenter of $A B C$ and let $Z$ be the foot of the perpendicular from $K$ on $E C$. Since $K B$ is the bisector of $\hat{B}$, then $\angle E B C=15^{\circ}$ and since $E M$ is the perpendicular bisector of $B C$, then $\angle E C B=\angle E B C=15^{\circ}$. Therefore $\angle K E C=30^{\circ}$. Moreover, $\angle E C K=60^{\circ}-15^{\circ}=45^{\circ}$. This means that $K Z C$ is isosceles and thus $Z$ is on the perpendicular bisector of $K C$.
Since $\angle K I C$ is the external angle of triangle $I B C$, and $I$ is the incenter of triangle $A B C$, then $\angle K I C=15^{\circ}+30^{\circ}=45^{\circ}$. Thus, $\angle K I C=\frac{\angle K Z C}{2}$. Since also $Z$ is on the perpendicular bisector of $K C$, then $Z$ is the circumcenter of $I K C$. This means that $Z K=Z I=Z C$. Since also $\angle E K Z=60^{\circ}$, then the triangle $Z K I$ is equilateral. Moreover, since $\angle K E Z=30^{\circ}$, we have that $Z K=\frac{E K}{2}$, so $Z K=I K=I E$.
Therefore $D I$ is perpendicular to $E K$ and this means that $D I K A$ is cyclic. So $\angle K D I=$ $\angle I A K=45^{\circ}$ and $\angle I K D=\angle I A D=45^{\circ}$. Thus $I D=I K=I E$ and so $K D$ is perpendicular to $D E$ as required.
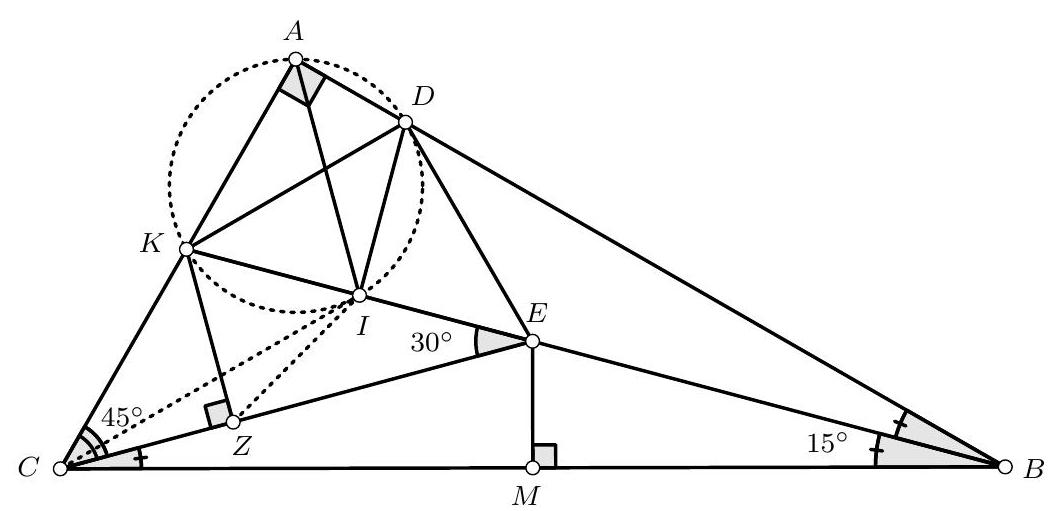
Alternative Question by Proposers. We can instead ask to prove that $E D=2 A D$. (After proving $K D \perp D E$ we have that the triangle $E D K$ is right angled and isosceles, therefore $E D=D K=2 A D$.) This alternative is probably more difficult because the perpendicular relation is hidden.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 76 |
G2. Let $A B C$ be a triangle and let $\omega$ be its circumcircle. Let $\ell_{B}$ and $\ell_{C}$ be two parallel lines passing through $B$ and $C$ respectively. The lines $\ell_{B}$ and $\ell_{C}$ intersect with $\omega$ for the second time at the points $D$ and $E$ respectively, with $D$ belonging on the arc $A B$, and $E$ on the arc $A C$. Suppose that $D A$ intersects $\ell_{C}$ at $F$, and $E A$ intersects $\ell_{B}$ at $G$. If $O, O_{1}$ and $O_{2}$ are the circumcenters of the triangles $A B C, A D G$ and $A E F$ respectively, and $P$ is the center of the circumcircle of the triangle $O O_{1} O_{2}$, prove that $O P$ is parallel to $\ell_{B}$ and $\ell_{C}$.
|
Solution. We write $\omega_{1}, \omega_{2}$ and $\omega^{\prime}$ for the circumcircles of $A G D, A E F$ and $O O_{1} O_{2}$ respectively. Since $O_{1}$ and $O_{2}$ are the centers of $\omega_{1}$ and $\omega_{2}$, and because $D G$ and $E F$ are parallel, we get that
$$
\angle G A O_{1}=90^{\circ}-\frac{\angle G O_{1} A}{2}=90^{\circ}-\angle G D A=90^{\circ}-\angle E F A=90^{\circ}-\frac{\angle E O_{2} A}{2}=\angle E A O_{2}
$$
So, because $G, A$ and $E$ are collinear, we come to the conclusion that $O_{1}, A$ and $O_{2}$ are also collinear.
Let $\angle D F E=\varphi$. Then, as a central angle $\angle A O_{2} E=2 \varphi$. Because $A E$ is a common chord of both $\omega$ and $\omega_{2}$, the line $O O_{2}$ that passes through their centers bisects $\angle A O_{2} E$, thus $\angle A O_{2} O=\varphi$. By the collinearity of $O_{1}, A, O_{2}$, we get that $\angle O_{1} O_{2} O=\angle A O_{2} O=\varphi$. As a central angle in $\omega^{\prime}$, we have $\angle O_{1} P O=2 \varphi$, so $\angle P O O_{1}=90^{\circ}-\varphi$. Let $Q$ be the point of intersection of $D F$ and $O P$. Because $A D$ is a common chord of $\omega$ and $\omega_{1}$, we have that $O O_{1}$ is perpendicular to $D A$ and so $\angle D Q P=90^{\circ}-\angle P O O_{1}=\varphi$. Thus, $O P$ is parallel to $\ell_{C}$ and so to $\ell_{B}$ as well.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 77 |
G3. Let $A B C$ be a triangle with incenter $I$. The points $D$ and $E$ lie on the segments $C A$ and $B C$ respectively, such that $C D=C E$. Let $F$ be a point on the segment $C D$. Prove that the quadrilateral $A B E F$ is circumscribable if and only if the quadrilateral $D I E F$ is cyclic.
|
Solution. Since $C D=C E$ it means that $E$ is the reflection of $D$ on the bisector of $\angle A C B$, i.e. the line $C I$. Let $G$ be the reflection of $F$ on $C I$. Then $G$ lies on the segment $C E$, the segment $E G$ is the reflection of the segment $D F$ on the line $C I$. Also, the quadraliteral $D E G F$ is cyclic since $\angle D F E=\angle E G D$.
Suppose that the quadrilateral $A B E F$ is circumscribable. Since $\angle F A I=\angle B A I$ and $\angle E B I=\angle A B I$, then $I$ is the centre of its inscribed circle. Then $\angle D F I=\angle E F I$ and since segment $E G$ is the reflection of segment $D F$ on the line $C I$, we have $\angle E F I=$ $\angle D G I$. So $\angle D F I=\angle D G I$ which means that quadrilateral $D I G F$ is cyclic. Since the quadrilateral $D E G F$ is also cyclic, we have that the quadrilateral $D I E F$ is cyclic.
Suppose that the quadrilateral $D I E F$ is cyclic. Since quadrilateral $D E G F$ is also cyclic, we have that the pentagon $D I E G F$ is cyclic. So $\angle I E B=180^{\circ}-\angle I E G=\angle I D G$ and since segment $E G$ is the reflection of segment $D F$ on the line $C I$, we have $\angle I D G=$ $\angle I E F$. Hence $\angle I E B=\angle I E F$, which means that $E I$ is the angle bisector of $\angle B E F$. Since $\angle I F A=\angle I F D=\angle I G D$ and since the segment $E G$ is the reflection of segment $D F$ on the line $C I$, we have $\angle I G D=\angle I F E$, hence $\angle I F A=\angle I F E$, which means that $F I$ is the angle bisector of $\angle E F A$. We also know that $A I$ and $B I$ are the angle bisectors of $\angle F A B$ and $\angle A B E$. So all angle bisectors of the quadrilateral $A B E F$ intersect at $I$, which means that it is circumscribable.
Comment by PSC. There is no need for introducing the point $G$. One can show that triangles $C I D$ and $C I E$ are equal and also that the triangles $C D M$ and $C E M$ are equal, where $M$ is the midpoint of $D E$. From these, one can deduce that $\angle C D I=\angle C E I$ and $\angle I D E=\angle I E D$ and proceed with similar reasoning as in the solution.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 78 |
G4. Let $A B C$ be a triangle such that $A B \neq A C$, and let the perpendicular bisector of the side $B C$ intersect lines $A B$ and $A C$ at points $P$ and $Q$, respectively. If $H$ is the orthocenter of the triangle $A B C$, and $M$ and $N$ are the midpoints of the segments $B C$ and $P Q$ respectively, prove that $H M$ and $A N$ meet on the circumcircle of $A B C$.
|
Solution. We have
$$
\angle A P Q=\angle B P M=90^{\circ}-\angle M B P=90^{\circ}-\angle C B A=\angle H C B
$$
and
$$
\angle A Q P=\angle M Q C=90^{\circ}-\angle Q C M=90^{\circ}-\angle A C B=\angle C B H
$$
From these two equalities, we see that the triangles $A P Q$ and $H C B$ are similar. Moreover, since $M$ and $N$ are the midpoints of the segments $B C$ and $P Q$ respectively, then the triangles $A Q N$ and $H B M$ are also similar. Therefore, we have $\angle A N Q=\angle H M B$.
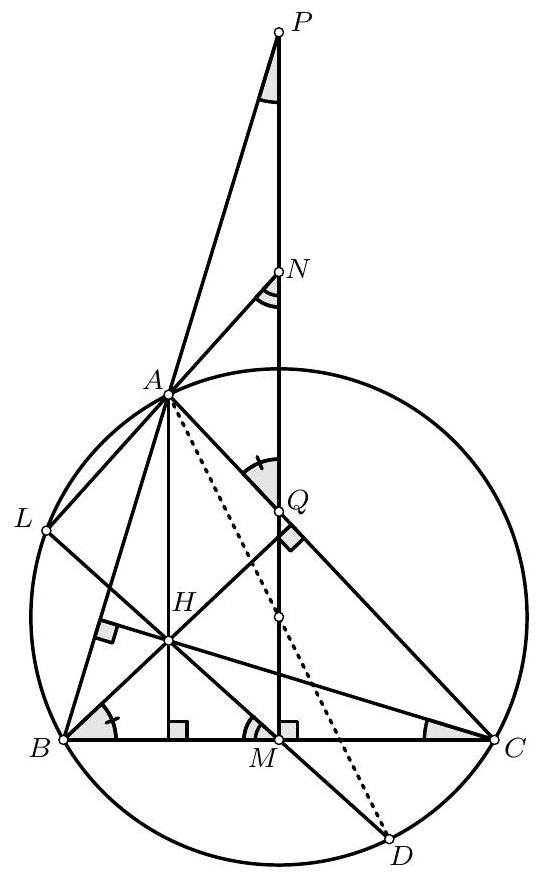
Let $L$ be the intersection of $A N$ and $H M$. We have
$\angle M L N=180^{\circ}-\angle L N M-\angle N M L=180^{\circ}-\angle L M B-\angle N M L=180^{\circ}-\angle N M B=90^{\circ}$.
Now let $D$ be the point on the circumcircle of $A B C$ diametrically oposite to $A$. It is known that $D$ is also the relfection of point $H$ over the point $M$. Therefore, we have that $D$ belongs on $M H$ and that $\angle D L A=\angle M L A=\angle M L N=90^{\circ}$. But, as $D A$ is the diameter of the circumcirle of $A B C$, the condition that $\angle D L A=90^{\circ}$ is enough to conclude that $L$ belongs on the circumcircle of $A B C$.
Remark by PSC. There is a spiral similarity mapping $A Q P$ to $H B C$. Since the similarity maps $A N$ to $H M$, it also maps $A H$ to $N M$, and since these two lines are parallel, the centre of the similarity is $L=A N \cap H M$. Since the similarity maps $B C$ to $Q P$, its centre belongs on the circumcircle of $B C X$, where $X=B Q \cap P C$. But $X$ is the reflection of $A$ on $Q M$ and so it must belong on the circumcircle of $A B C$. Hence so must $L$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 79 |
G5. Let $P$ be a point in the interior of a triangle $A B C$. The lines $A P, B P$ and $C P$ intersect again the circumcircles of the triangles $P B C, P C A$, and $P A B$ at $D, E$ and $F$ respectively. Prove that $P$ is the orthocenter of the triangle $D E F$ if and only if $P$ is the incenter of the triangle $A B C$.
|
Solution. If $P$ is the incenter of $A B C$, then $\angle B P D=\angle A B P+\angle B A P=\frac{\hat{A}+\hat{B}}{2}$, and $\angle B D P=\angle B C P=\frac{\hat{C}}{2}$. From triangle $B D P$, it follows that $\angle P B D=90^{\circ}$, i.e. that $E B$ is one of the altitudes of the triangle $D E F$. Similarly, $A D$ and $C F$ are altitudes, which means that $P$ is the orhocenter of $D E F$.
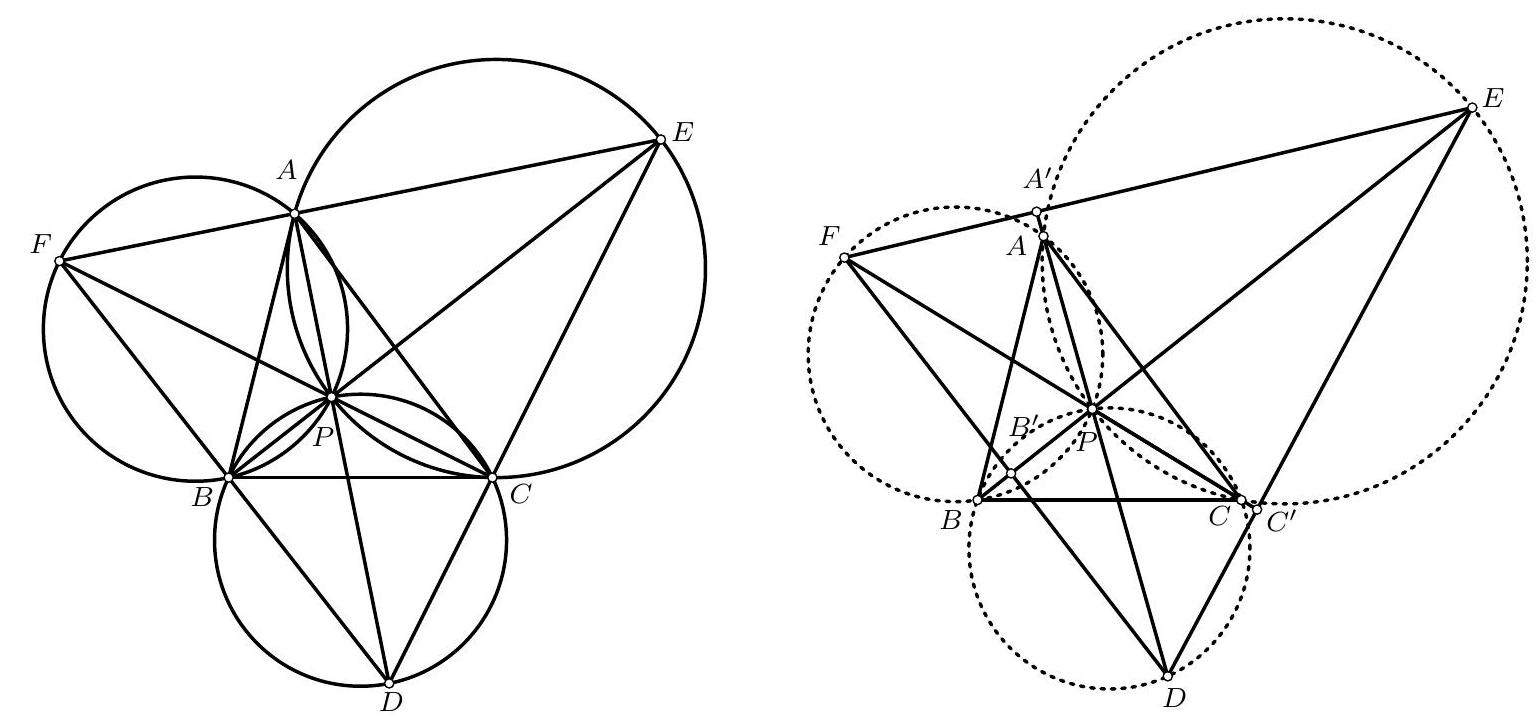
Notice that $A P$ separates $B$ from $C, B$ from $E$ and $C$ from $F$. Therefore $A P$ separates $E$ from $F$, which means that $P$ belongs to the interior of $\angle E D F$. It follows that $P \in$ $\operatorname{Int}(\triangle D E F)$.
If $P$ is the orthocenter of $D E F$, then clearly $D E F$ must be acute. Let $A^{\prime} \in E F, B^{\prime} \in D F$ and $C^{\prime} \in D E$ be the feet of the altitudes. Then the quadrilaterals $B^{\prime} P A^{\prime} F, C^{\prime} P B^{\prime} D$, and $A^{\prime} P C^{\prime} E$ are cyclic, which means that $\angle B^{\prime} F A^{\prime}=180^{\circ}-\angle B^{\prime} P A^{\prime}=180^{\circ}-\angle B P A=$ $\angle B F A$. Similarly, one obtains that $\angle C^{\prime} D B^{\prime}=\angle C D B$, and $\angle A^{\prime} E C^{\prime}=\angle A E C$.
- If $B \in \operatorname{Ext}(\triangle F P D)$, then $A \in \operatorname{Int}(\triangle E P F), C \in \operatorname{Ext}(\triangle D P E)$, and thus $B \in$ $\operatorname{Int}(\triangle F P D)$, contradiction.
- If $B \in \operatorname{Int}(\triangle F P D)$, then $A \in \operatorname{Ext}(\triangle E P F), C \in \operatorname{Int}(\triangle D P E)$, and thus $B \in$ $\operatorname{Ext}(\triangle F P D)$, contradiction.
This leaves us with $B \in F D$. Then we must have $A \in E F, C \in D E$, which means that $A=A^{\prime}, B=B^{\prime}, C=C^{\prime}$. Thus $A B C$ is the orthic triangle of triangle $D E F$ and it is well known that the orthocenter of an acute triangle $D E F$ is the incenter of its orthic triangle.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 80 |
G6. Let $A B C$ be a non-isosceles triangle with incenter $I$. Let $D$ be a point on the segment $B C$ such that the circumcircle of $B I D$ intersects the segment $A B$ at $E \neq B$, and the circumcircle of $C I D$ intersects the segment $A C$ at $F \neq C$. The circumcircle of $D E F$ intersects $A B$ and $A C$ at the second points $M$ and $N$ respectively. Let $P$ be the point of intersection of $I B$ and $D E$, and let $Q$ be the point of intersection of $I C$ and $D F$. Prove that the three lines $E N, F M$ and $P Q$ are parallel.
|
Solution. Since $B D I E$ is cyclic, and $B I$ is the bisector of $\angle D B E$, then $I D=I E$. Similarly, $I D=I F$, so $I$ is the circumcenter of the triangle $D E F$. We also have
$$
\angle I E A=\angle I D B=\angle I F C
$$
which implies that $A E I F$ is cyclic. We can assume that $A, E, M$ and $A, N, F$ are collinear in that order. Then $\angle I E M=\angle I F N$. Since also $I M=I E=I N=I F$, the two isosceles triangles $I E M$ and $I N F$ are congruent, thus $E M=F N$ and therefore $E N$ is parallel to $F M$. From that, we can also see that the two triangles $I E A$ and $I N A$ are congruent, which implies that $A I$ is the perpendicular bisector of $E N$ and $M F$.
Note that $\angle I D P=\angle I D E=\angle I B E=\angle I B D$, so the triangles $I P D$ and $I D B$ are similar, which implies that $\frac{I D}{I B}=\frac{I P}{I D}$ and $I P \cdot I B=I D^{2}$. Similarly, we have $I Q \cdot I C=I D^{2}$, thus $I P \cdot I B=I Q \cdot I C$. This implies that $B P Q C$ is cyclic, which leads to
$$
\angle I P Q=\angle I C B=\frac{\hat{C}}{2}
$$
But $\angle A I B=90^{\circ}+\frac{\hat{C}}{2}$, so $A I$ is perpendicular to $P Q$. Hence, $P Q$ is parallel to $E N$ and FM.
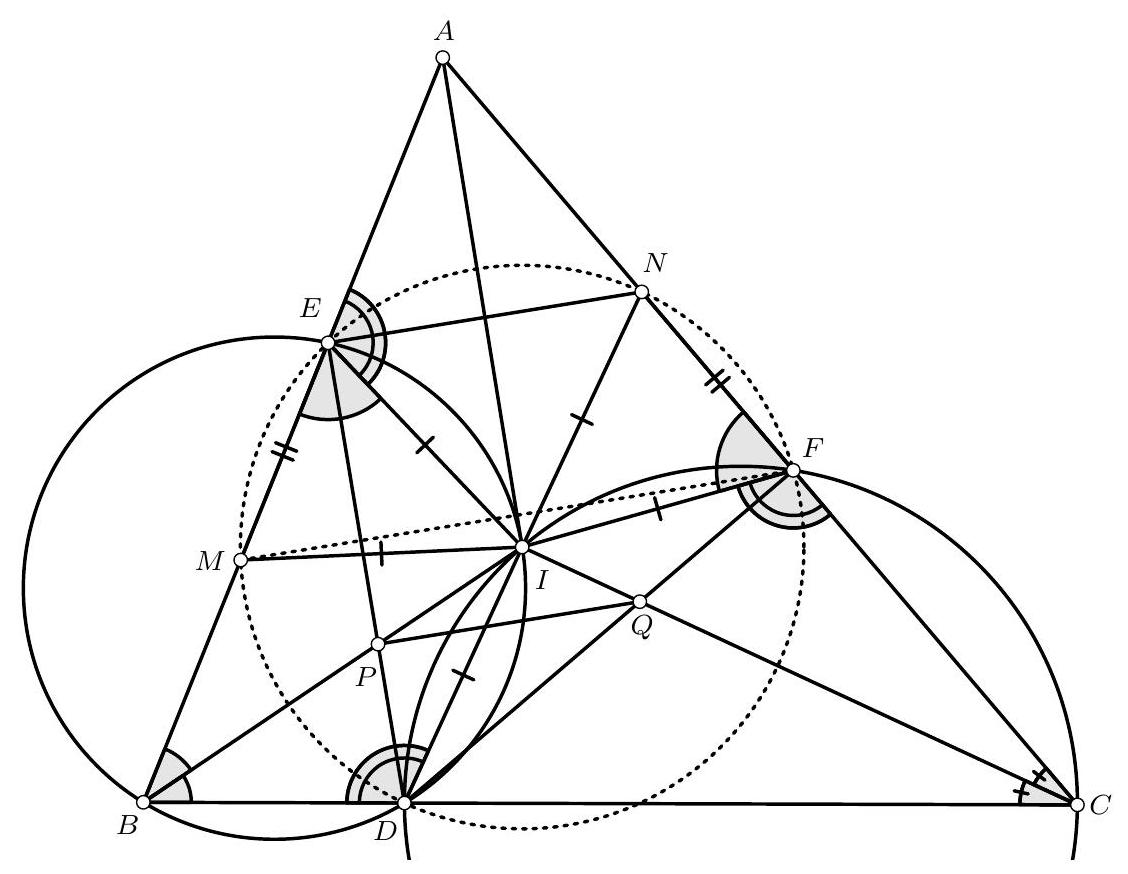
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 81 |
G7. Let $A B C$ be a right-angled triangle with $\hat{A}=90^{\circ}$. Let $K$ be the midpoint of $B C$, and let $A K L M$ be a parallelogram with centre $C$. Let $T$ be the intersection of the line $A C$ and the perpendicular bisector of $B M$. Let $\omega_{1}$ be the circle with centre $C$ and radius $C A$ and let $\omega_{2}$ be the circle with centre $T$ and radius $T B$. Prove that one of the points of intersection of $\omega_{1}$ and $\omega_{2}$ is on the line $L M$.
|
Solution. Let $M^{\prime}$ be the symmetric point of $M$ with respect to $T$. Observe that $T$ is equidistant from $B$ and $M$, therefore $M$ belongs on $\omega_{2}$ and $M^{\prime} M$ is a diameter of $\omega_{2}$. It suffices to prove that $M^{\prime} A$ is perpendicular to $L M$, or equivalently, to $A K$. To see this, let $S$ be the point of intersection of $M^{\prime} A$ with $L M$. We will then have $\angle M^{\prime} S M=90^{\circ}$ which shows that $S$ belongs on $\omega_{2}$ as $M^{\prime} M$ is a diameter of $\omega_{2}$. We also have that $S$ belongs on $\omega_{1}$ as $A L$ is diameter of $\omega_{1}$.
Since $T$ and $C$ are the midpoints of $M^{\prime} M$ and $K M$ respectively, then $T C$ is parallel to $M^{\prime} K$ and so $M^{\prime} K$ is perpendicular to $A B$. Since $K A=K B$, then $K M^{\prime}$ is the perpendicular bisector of $A B$. But then the triangles $K B M^{\prime}$ and $K A M^{\prime}$ are equal, showing that $\angle M^{\prime} A K=\angle M^{\prime} B K=\angle M^{\prime} B M=90^{\circ}$ as required.
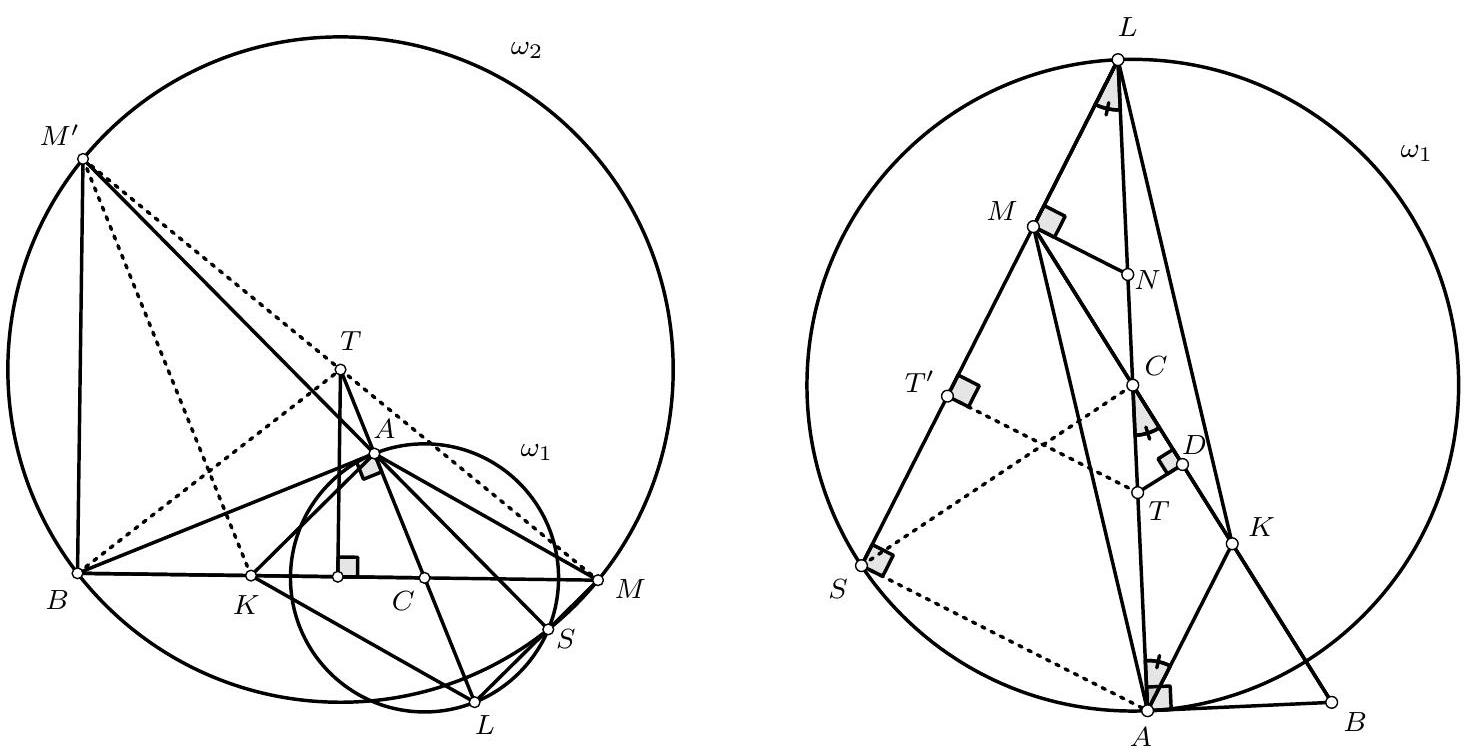
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 82 |
G1 Let $A B C$ be an isosceles triangle with $A B=A C$. On the extension of the side $[C A]$ we consider the point $D$ such that $A D<A C$. The perpendicular bisector of the segment $[B D]$ meets the internal and the external bisectors of the angle $\widehat{B A C}$ at the points $E$ and $Z$, respectively. Prove that the points $A, E, D, Z$ are concyclic.
|
Solution 1
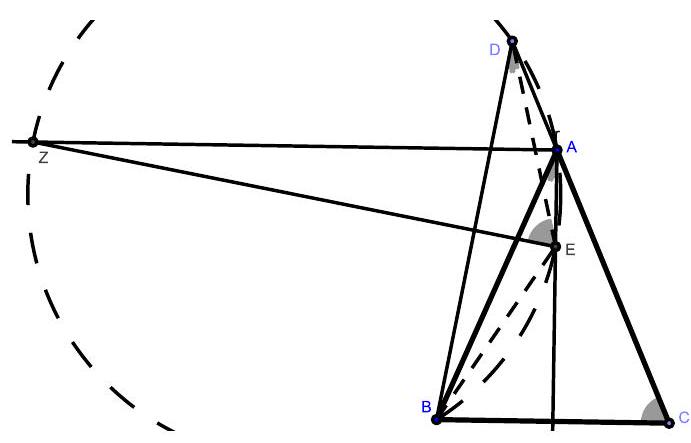
In $\triangle A B D$ the ray $[A Z$ bisects the angle $\widehat{D A B}$ and the line $Z E$ is the perpendicular bisector of the side $[B D]$. Hence $Z$ belongs to the circumcircle of $\triangle A B D$.
Therefore the points $A, B, D, Z$ are concyclic.
In $\triangle B C D, A E$ and $Z E$ are the perpendicular bisectors $[B C]$ and $[B D]$, respectively. Hence, $E$ is the circumcenter of $\triangle B C D$ and therefore $\widehat{D E Z}=\widehat{B E D} / 2=\widehat{A C B}$. Since $B D \perp Z E$, we conclude that: $\widehat{B D E}=90^{\circ}-\widehat{D E Z}=90^{\circ}-\widehat{A C B}=\widehat{B A E}$. Hence the quadrilateral $A E B D$ is cyclic, that is the points $A, B, D, E$ are concyclic. Therefore, since $A, B, D, Z$ are also concyclic, we conclude that $A E Z D$ is cyclic.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 83 |
G6 Let $A B C D$ be a convex quadrilateral, $E$ and $F$ points on the sides $A B$ and $C D$, respectively, such that $\frac{A B}{A E}=\frac{C D}{D F}=n$. Denote by $S$ the area of the quadrilateral $A E F D$. Prove that $S \leq \frac{A B \cdot C D+n(n-1) \cdot D A^{2}+n \cdot A D \cdot B C}{2 n^{2}}$.
|
## Solution
By Ptolemy's Inequality in $A E F D$, we get $S=\frac{A F \cdot D E \cdot \sin (\widehat{A F, D E})}{2} \leq \frac{A F \cdot D E}{2} \leq$ $\frac{A E \cdot D F+A D \cdot E F}{2}=\frac{A B \cdot C D+n^{2} \cdot D A \cdot E F}{2 n^{2}}$.
Let $G$ be a point on diagonal $B D$ such that $\frac{D B}{D G}=n$. By Thales's Theorem we get $G E=\frac{(n-1) A D}{n}$ and $G F=\frac{B C}{n}$. Applying the inequality of triangle in $\triangle E G F$ we get $E F \leq E G+G F=\frac{(n-1) A D+B C}{n}$. Now, we get:
$S \leq \frac{A B \cdot C D+n^{2} A D \cdot E F}{2 n^{2}} \leq \frac{A B \cdot C D+n(n-1) \cdot D A^{2}+n \cdot A D \cdot B C}{2 n^{2}}$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 84 |
NT1. Let $a, b, p, q$ be positive integers such that $a$ and $b$ are relatively prime, $a b$ is even and $p, q \geq 3$. Prove that
$$
2 a^{p} b-2 a b^{q}
$$
$$
a \text { is even }
$$
cannot be a square of an integer number.
|
Solution. Without loss of
Let $a=2 a^{\prime}$. If $\vdots$. Without loss of generality, assume that $a$ is even and consequently $b$ is odd.
$$
2 a^{p} b-2 a b^{q}=4 a^{\prime} b\left(a^{p-1}-b^{q-1}\right)
$$
is a square, then $a^{\prime}, b$ and $a^{p-1}-b^{q-1}$ are pairwise coprime.
On the other hand, $a^{p-1}$ is divisible by 4 and $b^{q-1}$ gives the remainder 1 when divided by 4. It follows that $a^{p-1}-b^{q-1}$ has the form $4 k+3$, a contradiction.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 85 |
NT4. If the positive integers $x$ and $y$ are such that both $3 x+4 y$ and $4 x+3 y$ are perfect squares, prove that both $x$ and $y$ are multiples of 7 .
|
Solution. Let
$$
3 x+4 y=m^{2}, \quad 4 x+3 y=n^{2}
$$
Then
$$
7(x+y)=m^{2}+n^{2} \Rightarrow 7 \mid m^{2}+n^{2}
$$
Considering $m=7 k+r, \quad r \in\{0,1,2,3,4,5,6\}$ we find that $m^{2} \equiv u(\bmod 7), \quad u \in$ $\{0,1,2,4\}$ and similarly $n^{2} \equiv v(\bmod 7), \quad v \in\{0,1,2,4\}$. Therefore we have either $m^{2}+n^{2} \equiv 0 \quad(\bmod 7)$, when $u=v=0$, or $m^{2}+n^{2} \equiv w(\bmod 7), w \in\{1,2,3,4,5,6\}$. However, from (2) we have that $m^{2}+n^{2} \equiv 0(\bmod \tau)$ and hence $u=v=0$ and
$$
m^{2}+n^{2} \equiv 0 \quad\left(\bmod \tau^{2}\right) \Rightarrow 7(x+y) \equiv 0 \quad\left(\bmod \tau^{2}\right)
$$
and cousequently
$$
x+y \equiv 0 \quad(\bmod 7)
$$
Moreover. from (1) we have $x-y=n^{2}-m^{2}$ and $n^{2}-m^{2} \equiv 0\left(\bmod i^{2}\right)$ (since $\left.u=c=0\right)$, so
$$
x-y \equiv 0 \quad(\bmod 7) .
$$
From (3) and (4) we have tliat $x+y=7 k, x-y=7 l$, where $k$ and $l$ are positive incegers. Hence
$$
2 x=7(k+l), 2 y=7(k-l)
$$
where $k+l$ and $k-l$ are positive integers. It follows that $i \mid 2 x$ and $i \mid 2 y$, and finally $\pi \mid x$ and i|y.
## ALGEBRA
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 86 |
A1. Prove that
$$
(1+a b c)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \geq 3+a+b+c
$$
for any real numbers $a, b, c \geq 1$.
|
Solution. The inequality rewrites as
$$
\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)+(b c+a c+a b) \geq 3+a+b+c
$$
or
$$
\left(\frac{\frac{1}{a}+\frac{1}{b}}{2}+\frac{\frac{1}{b}+\frac{1}{c}}{2}+\frac{\frac{1}{a}+\frac{1}{c}}{2}\right)+(b c+a c+a b) \geq 3+a+b+c
$$
which is equivalent to
$$
\frac{(2 a b-(a+b))(a b-1)}{2 a b}+\frac{(2 b c-(b+c))(b c-1)}{2 b c}+\frac{(2 c a-(c+a))(c a-1)}{2 c a} \geq 0
$$
The last inequality is true due to the obvious relations
$$
2 x y-(x+y)=x(y-1)+y(x-1) \geq 0
$$
for any two real numbers $x, y \geq 1$.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 87 |
A2. Prove that, for all real numbers $x, y, z$ :
$$
\frac{x^{2}-y^{2}}{2 x^{2}+1}+\frac{y^{2}-z^{2}}{2 y^{2}+1}+\frac{z^{2}-x^{2}}{2 z^{2}+1} \leq(x+y+z)^{2}
$$
When the equality holds?
|
Solution. For $x=y=z=0$ the equality is valid.
Since $(x+y+z)^{2} \geq 0$ it is enongh to prove that
$$
\frac{x^{2}-y^{2}}{2 x^{2}+1}+\frac{y^{2}-z^{2}}{2 y^{2}+1}+\frac{z^{2}-x^{2}}{2 z^{2}+1} \leq 0
$$
which is equivalent to the inequality
$$
\frac{x^{2}-y^{2}}{x^{2}+\frac{1}{2}}+\frac{y^{2}-z^{2}}{y^{2}+\frac{1}{2}}+\frac{z^{2}-x^{2}}{z^{2}+\frac{1}{2}} \leq 0
$$
Dellote
$$
a=x^{2}+\frac{1}{2}, b=y^{2}+\frac{1}{2}, c=z^{2}+\frac{1}{2}
$$
Then (1) is equivalent to
$$
\frac{a-b}{a}+\frac{b-c}{b}+\frac{c-a}{c} \leq 0
$$
From very well known $A G$ inequality follows that
$$
a^{2} b+b^{2} c+c^{2} a \geq 3 a b c
$$
Fron the equivalencies
$$
a^{2} b+b^{2} c+c^{2} a \geq 3 a b c \Leftrightarrow \frac{a}{c}+\frac{b}{a}+\frac{c}{b} \geq-3 \Leftrightarrow \frac{a-b}{a}+\frac{b-c}{b}+\frac{c-a}{c} \leq 0
$$
follows thait the inequality (2) is valid, for positive real numbers $a, b, c$.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 88 |
A3. Prove that for all real $x, y$
$$
\frac{x+y}{x^{2}-x y+y^{2}} \leq \frac{2 \sqrt{2}}{\sqrt{x^{2}+y^{2}}}
$$
|
Solution. The inequality rewrites as
$$
\frac{x+y}{x^{2}-x y+y^{2}} \leq \frac{\sqrt{2\left(x^{2}+y^{2}\right)}}{\frac{x^{2}+y^{2}}{2}}
$$
Now it is enough to prove the next two simple inequalities:
$$
x+y \leq \sqrt{2\left(x^{2}+y^{2}\right)}, \quad x^{2}-x y+y^{2} \geq \frac{x^{2}+y^{2}}{2}
$$
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 89 |
A4. Prove that if $0<\frac{a}{b}<b<2 a$ then
$$
\frac{2 a b-a^{2}}{7 a b-3 b^{2}-2 a^{2}}+\frac{2 a b-b^{2}}{7 a b-3 a^{2}-2 b^{2}} \geq 1+\frac{1}{4}\left(\frac{a}{b}-\frac{b}{a}\right)^{2}
$$
|
Solution. If we denote
$$
u=2-\frac{a}{b}, \quad v=2-\frac{b}{a}
$$
then the inequality rewrites as
$$
\begin{aligned}
& \frac{u}{v+u v}+\frac{v}{u+u v} \geq 1+\frac{1}{4}(u-u)^{2} \\
& \frac{(u-v)^{2}+u v(1-u v)}{u v(u v+u+v+1)} \geq \frac{(u-u)^{2}}{4}
\end{aligned}
$$
$\mathrm{Or}$
Since $u>0, v>0, u+v \leq 2, u v \leq 1, u v(u+v+u v+1) \leq 4$, the result is clear.
## GEOMETRY
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 90 |
G5. Let $A B C$ be a triangle with $\angle C=90^{\circ}$ and $D \in C .4, E \in C^{\prime} B$, and $k_{1}, k_{2}, k_{3}, k_{4}$ semicircles with diameters $C A, C B, C D, C E$ respectively, which have common part with the triangle $A B C$. Let also,
$$
k_{1} \cap k_{2}=\{C, K\}, k_{3} \cap k_{4}=\{C, M\}, k_{2} \cap k_{3}=\{C, L\}, k_{1} \cap k_{4}=\{C, N\}
$$
Prove that $K, L, M$ and $N$ are cocyclic points.
|
Solution. The points $K, L, M, N$ belong to the segments $A B, B D, D E, E A$ respectively, where $C K \perp A B, C L \perp B D, C M \perp D E, C N \perp A E$. Then quadrilaterals $C D L M$ and $C E N M$ are inscribed. Let $\angle C A E=\varphi, \angle D C L=\theta$. Then $\angle E M N=\angle E C N=\varphi$ and $\angle D M L=\angle D C L=\theta$. So $\angle D M L+\angle E M N=\varphi+\theta$ and therefore $\angle L M N=180^{\circ}-\varphi-\theta$. The quadrilaterals $C B K L$ and $C A K N$ are also inscribed and hence $\angle L K C=\angle L B C=\theta$, $\angle C K N=\angle C A N=\varphi$, and so $\angle L K N=\varphi+\theta$, while $\angle L M N=180^{\circ}-\varphi-\theta$, which means that $K L M N$ is inscribed.
Note that $K L M N$ is convex because $L, N$ lie in the interior of the convex quadrilateral $A D E B$.
## COMBINATORICS
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 93 |
Problem A1. The real numbers $a, b, c, d$ satisfy simultaneously the equations
$$
a b c-d=1, b c d-a=2, c d a-b=3, d a b-c=-6
$$
Prove that $a+b+c+d \neq 0$.
|
Solution. Suppose that $a+b+c+d=0$. Then
$$
a b c+b c d+c d a+d a b=0
$$
If $a b c d=0$, then one of numbers, say $d$, must be 0 . In this case $a b c=0$, and so at least two of the numbers $a, b, c, d$ will be equal to 0 , making one of the given equations impossible. Hence $a b c d \neq 0$ and, from (1),
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}=0
$$
implying
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}
$$
It follows that $(a+b)(b+c)(c+a)=0$, which is impossible (for instance, if $a+b=0$, then adding the second and third given equations would lead to $0=2+3$, a contradiction). Thus $a+b+c+d \neq 0$.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 96 |
Problem A4. Let $a, b, c$ be positive real numbers such that $a b c(a+b+c)=3$. Prove the inequality
$$
(a+b)(b+c)(c+a) \geq 8
$$
and determine all cases when equality holds.
|
Solution. We have
$A=(a+b)(b+c)(c+a)=\left(a b+a c+b^{2}+b c\right)(c+a)=(b(a+b+c)+a c)(c+a)$,
so by the given condition
$$
A=\left(\frac{3}{a c}+a c\right)(c+a)=\left(\frac{1}{a c}+\frac{1}{a c}+\frac{1}{a c}+a c\right)(c+a)
$$
Aplying the AM-GM inequality for four and two terms respectively, we get
$$
A \geq 4 \sqrt[4]{\frac{a c}{(a c)^{3}}} \cdot 2 \sqrt{a c}=8
$$
From the last part, it is easy to see that inequality holds when $a=c$ and $\frac{1}{a c}=a c$, i.e. $a=b=c=1$.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 97 |
Problem A5. The real positive numbers $x, y, z$ satisfy the relations $x \leq 2$, $y \leq 3, x+y+z=11$. Prove that $\sqrt{x y z} \leq 6$.
|
Solution. For $x=2, y=3$ and $z=6$ the equality holds.
After the substitutions $x=2-u, y=3-v$ with $u \in[0,2), v \in[0,3)$, we obtain that $z=6+u+v$ and the required inequality becomes
$$
(2-u)(3-v)(6+u+v) \leqslant 36
$$
We shall need the following lemma.
Lemma. If real numbers $a$ and $b$ satisfy the relations $00$ and $y \geq 0$.
The equality in (2) holds if $y=0$. The lemma is proved.
By using the lemma we can write the following inequalities:
$$
\begin{gathered}
\frac{6}{6+u} \geqslant \frac{2-u}{2} \\
\frac{6}{6+v} \geqslant \frac{3-v}{3} \\
\frac{6+u}{6+u+v} \geqslant \frac{6}{6+v}
\end{gathered}
$$
By multiplying the inequalities (3), (4) and (5) we obtain:
$$
\begin{gathered}
\frac{6 \cdot 6 \cdot(6+u)}{(6+u)(6+v)(6+u+v)} \geqslant \frac{6(2-u)(3-v)}{2 \cdot 3(6+v)} \Leftrightarrow \\
(2-u)(3-v)(6+u+v) \leqslant 2 \cdot 3 \cdot 6=36 \Leftrightarrow \quad(1)
\end{gathered}
$$
By virtue of lemma, the equality holds if and only if $u=v=0$.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 98 |
Problem G1. Consider a triangle $A B C$ with $\angle A C B=90^{\circ}$. Let $F$ be the foot of the altitude from $C$. Circle $\omega$ touches the line segment $F B$ at point $P$, the altitude $C F$ at point $Q$ and the circumcircle of $A B C$ at point $R$. Prove that points $A, Q, R$ are collinear and $A P=A C$.
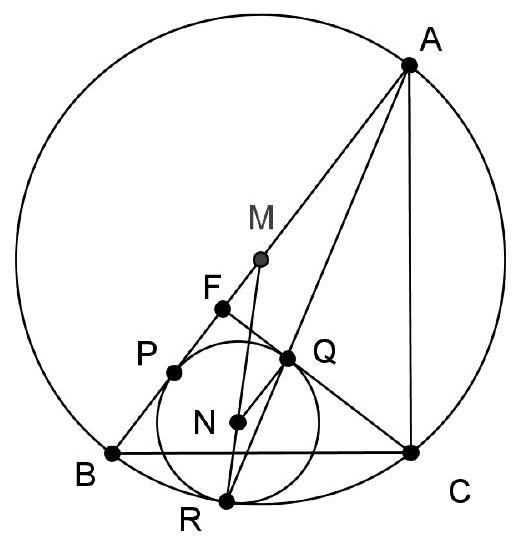
|
Solution. Let $M$ be the midpoint of $A B$ and let $N$ be the center of $\omega$. Then $M$ is the circumcenter of triangle $A B C$, so points $M, N$ and $R$ are collinear. From $Q N \| A M$ we get $\angle A M R=\angle Q N R$. Besides that, triangles $A M R$ and $Q N R$ are isosceles, therefore $\angle M R A=\angle N R Q$; thus points $A, Q, R$ are collinear.
Right angled triangles $A F Q$ and $A R B$ are similar, which implies $\frac{A Q}{A B}=\frac{A F}{A R}$, that is $A Q \cdot A R=A F \cdot A B$. The power of point $A$ with respect to $\omega$ gives $A Q \cdot A R=A P^{2}$. Also, from similar triangles $A B C$ and $A C F$ we get $A F \cdot A B=$ $A C^{2}$. Now, the claim follows from $A C^{2}=A F \cdot A B=A Q \cdot A R=A P^{2}$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 99 |
Problem G3. Let $A B C$ be an acute-angled triangle. A circle $\omega_{1}\left(O_{1}, R_{1}\right)$ passes through points $B$ and $C$ and meets the sides $A B$ and $A C$ at points $D$ and $E$, respectively. Let $\omega_{2}\left(O_{2}, R_{2}\right)$ be the circumcircle of the triangle $A D E$. Prove that $O_{1} O_{2}$ is equal to the circumradius of the triangle $A B C$.
|
Solution. Recall that, in every triangle, the altitude and the diameter of the circumcircle drawn from the same vertex are isogonal. The proof offers no difficulty, being a simple angle chasing around the circumcircle of the triangle.
Let $O$ be the circumcenter of the triangle $A B C$. From the above, one has $\angle O A E=90^{\circ}-B$. On the other hand $\angle D E A=B$, for $B C D E$ is cyclic. Thus $A O \perp D E$, implying that in the triangle $A D E$ cevians $A O$ and $A O_{2}$ are isogonal. So, since $A O$ is a radius of the circumcircle of triangle $A B C$, one obtains that $A O_{2}$ is an altitude in this triangle.
Moreover, since $O O_{1}$ is the perpendicular bisector of the line segment $B C$, one has $O O_{1} \perp B C$, and furthermore $A O_{2} \| O O_{1}$.
Chord $D E$ is common to $\omega_{1}$ and $\omega_{2}$, hence $O_{1} O_{2} \perp D E$. It follows that $A O \|$ $O_{1} O_{2}$, so $A O O_{1} O_{2}$ is a parallelogram. The conclusion is now obvious.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 100 |
A2. Given positive real numbers $a, b, c$, prove that
$$
\frac{8}{(a+b)^{2}+4 a b c}+\frac{8}{(a+c)^{2}+4 a b c}+\frac{8}{(b+c)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \geq \frac{8}{a+3}+\frac{8}{b+3}+\frac{8}{c+3}
$$
|
Solution. Since $2 a b \leq a^{2}+b^{2}$, it follows that $(a+b)^{2} \leq 2\left(a^{2}+b^{2}\right)$ and $4 a b c \leq 2 c\left(a^{2}+b^{2}\right)$, for any positive reals $a, b, c$. Adding these inequalities, we find
$$
(a+b)^{2}+4 a b c \leq 2\left(a^{2}+b^{2}\right)(c+1)
$$
so that
$$
\frac{8}{(a+b)^{2}+4 a b c} \geq \frac{4}{\left(a^{2}+b^{2}\right)(c+1)}
$$
Using the AM-GM inequality, we have
$$
\frac{4}{\left(a^{2}+b^{2}\right)(c+1)}+\frac{a^{2}+b^{2}}{2} \geq 2 \sqrt{\frac{2}{c+1}}=\frac{4}{\sqrt{2(c+1)}}
$$
respectively
$$
\frac{c+3}{8}=\frac{(c+1)+2}{8} \geq \frac{\sqrt{2(c+1)}}{4}
$$
We conclude that
$$
\frac{4}{\left(a^{2}+b^{2}\right)(c+1)}+\frac{a^{2}+b^{2}}{2} \geq \frac{8}{c+3}
$$
and finally
$\frac{8}{(a+b)^{2}+4 a b c}+\frac{8}{(a+c)^{2}+4 a b c}+\frac{8}{(b+c)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \geq \frac{8}{a+3}+\frac{8}{b+3}+\frac{8}{c+3}$.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 103 |
A4. If $x, y, z$ are non-negative real numbers such that $x^{2}+y^{2}+z^{2}=x+y+z$, then show that:
$$
\frac{x+1}{\sqrt{x^{5}+x+1}}+\frac{y+1}{\sqrt{y^{5}+y+1}}+\frac{z+1}{\sqrt{z^{5}+z+1}} \geq 3
$$
When does the equality hold?
|
Solution. First we factor $x^{5}+x+1$ as follows:
$$
\begin{aligned}
x^{5}+x+1 & =x^{5}-x^{2}+x^{2}+x+1=x^{2}\left(x^{3}-1\right)+x^{2}+x+1=x^{2}(x-1)\left(x^{2}+x+1\right)+x^{2}+x+1 \\
& =\left(x^{2}+x+1\right)\left(x^{2}(x-1)+1\right)=\left(x^{2}+x+1\right)\left(x^{3}-x^{2}+1\right)
\end{aligned}
$$
Using the $A M-G M$ inequality, we have
$$
\sqrt{x^{5}+x+1}=\sqrt{\left(x^{2}+x+1\right)\left(x^{3}-x^{2}+1\right)} \leq \frac{x^{2}+x+1+x^{3}-x^{2}+1}{2}=\frac{x^{3}+x+2}{2}
$$
and since
$x^{3}+x+2=x^{3}+1+x+1=(x+1)\left(x^{2}-x+1\right)+x+1=(x+1)\left(x^{2}-x+1+1\right)=(x+1)\left(x^{2}-x+2\right)$,
then
$$
\sqrt{x^{5}+x+1} \leq \frac{(x+1)\left(x^{2}-x+2\right)}{2}
$$
Using $x^{2}-x+2=\left(x-\frac{1}{2}\right)^{2}+\frac{7}{4}>0$, we obtain $\frac{x+1}{\sqrt{x^{5}+x+1}} \geq \frac{2}{x^{2}-x+2}$ Applying the CauchySchwarz inequality and the given condition, we get
$$
\sum_{c y c} \frac{x+1}{\sqrt{x^{5}+x+1}} \geq \sum_{c y c} \frac{2}{x^{2}-x+2} \geq \frac{18}{\sum_{c y c}\left(x^{2}-x+2\right)}=\frac{18}{6}=3
$$
which is the desired result.
For the equality both conditions: $x^{2}-x+2=y^{2}-y+2=z^{2}-z+2$ (equality in CBS) and $x^{3}-x^{2}+1=x^{2}+x+1$ (equality in AM-GM) have to be satisfied.
By using the given condition it follows that $x^{2}-x+2+y^{2}-y+2+z^{2}-z+2=6$, hence $3\left(x^{2}-x+2\right)=6$, implying $x=0$ or $x=1$. Of these, only $x=0$ satisfies the second condition. We conclude that equality can only hold for $x=y=z=0$.
It is an immediate check that indeed for these values equality holds.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 104 |
A5. Let $x, y, z$ be positive real numbers such that $x+y+z=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}$.
a) Prove the inequality
$$
x+y+z \geq \sqrt{\frac{x y+1}{2}}+\sqrt{\frac{y z+1}{2}}+\sqrt{\frac{z x+1}{2}}
$$
b) (Added by the problem selecting committee) When does the equality hold?
|
## Solution.
a) We rewrite the inequality as
$$
(\sqrt{x y+1}+\sqrt{y z+1}+\sqrt{z x+1})^{2} \leq 2 \cdot(x+y+z)^{2}
$$
and note that, from CBS,
$$
\text { LHS } \leq\left(\frac{x y+1}{x}+\frac{y z+1}{y}+\frac{z x+1}{z}\right)(x+y+z)
$$
But
$$
\frac{x y+1}{x}+\frac{y z+1}{y}+\frac{z x+1}{z}=x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=2(x+y+z)
$$
which proves (1).
b) The equality occurs when we have equality in CBS, i.e. when
$$
\frac{x y+1}{x^{2}}=\frac{y z+1}{y^{2}}=\frac{z x+1}{z^{2}}\left(=\frac{x y+y z+z x+3}{x^{2}+y^{2}+z^{2}}\right)
$$
Since we can also write
$$
(\sqrt{x y+1}+\sqrt{y z+1}+\sqrt{z x+1})^{2} \leq\left(\frac{x y+1}{y}+\frac{y z+1}{z}+\frac{z x+1}{x}\right)(y+z+x)=2(x+y+z)^{2}
$$
the equality implies also
$$
\frac{x y+1}{y^{2}}=\frac{y z+1}{z^{2}}=\frac{z x+1}{x^{2}}\left(=\frac{x y+y z+z x+3}{x^{2}+y^{2}+z^{2}}\right)
$$
But then $x=y=z$, and since $x+y+z=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}$, we conclude that $x=\frac{1}{x}=1=y=z$.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 105 |
G1. Let $A B C$ be an acute angled triangle, let $O$ be its circumcentre, and let $D, E, F$ be points on the sides $B C, A C, A B$, respectively. The circle $\left(c_{1}\right)$ of radius $F A$, centred at $F$, crosses the segment $(O A)$ at $A^{\prime}$ and the circumcircle (c) of the triangle $A B C$ again at $K$. Similarly, the circle $\left(c_{2}\right)$ of radius $D B$, centred at $D$, crosses the segment $(O B)$ at $B^{\prime}$ and the circle (c) again at $L$. Finally, the circle $\left(c_{3}\right)$ of radius $E C$, centred at $E$, crosses the segment $(O C)$ at $C^{\prime}$ and the circle (c) again at $M$. Prove that the quadrilaterals $B K F A^{\prime}$, $C L D B^{\prime}$ and $A M E C^{\prime}$ are all cyclic, and their circumcircles share a common point.
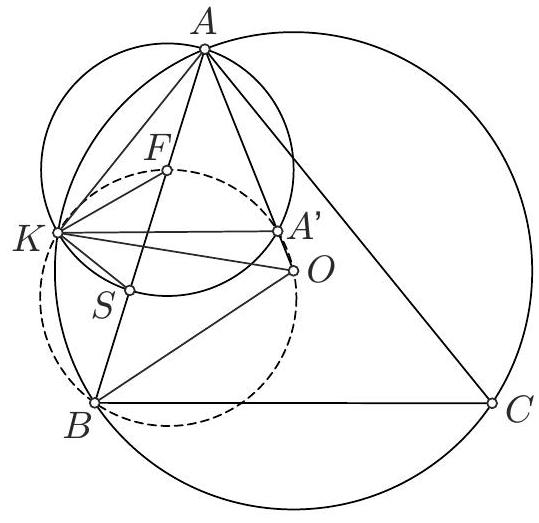
|
Solution. We will prove that the quadrilateral $B K F A^{\prime}$ is cyclic and its circumcircle passes through the center $O$ of the circle (c).
The triangle $A F K$ is isosceles, so $m(\widehat{K F B})=2 m(\widehat{K A B})=m(\widehat{K O B})$. It follows that the quadrilateral $B K F O$ is cyclic.
The triangles $O F K$ and $O F A$ are congruent (S.S.S.), hence $m(\widehat{O K F})=m(\widehat{O A F})$. The triangle $F A A^{\prime}$ is isosceles, so $m\left(\widehat{F A^{\prime} A}\right)=m(\widehat{O A F})$. Therefore $m\left(\widehat{F A^{\prime} A}\right)=m(\widehat{O K F})$, so the quadrilateral $O K F A^{\prime}$ is cyclic.
(1) and (2) prove the initial claim.
Along the same lines, we can prove that the points $C, D, L, B^{\prime}, O$ and $A, M, E, C^{\prime}, O$ are concylic, respectively, so their circumcircles also pass through $O$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 106 |
G2. Let $A B C$ be a triangle with $m(\widehat{B A C})=60^{\circ}$. Let $D$ and $E$ be the feet of the perpendiculars from $A$ to the external angle bisectors of $\widehat{A B C}$ and $\widehat{A C B}$, respectively. Let $O$ be the circumcenter of the triangle $A B C$. Prove that the circumcircles of the triangles $\triangle A D E$ and $\triangle B O C$ are tangent to each other.
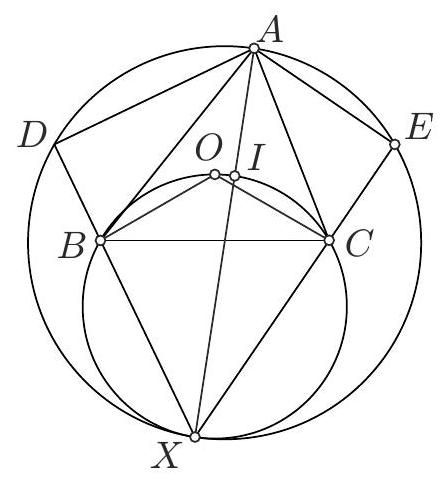
|
Solution. Let $X$ be the intersection of the lines $B D$ and $C E$.
We will prove that $X$ lies on the circumcircles of both triangles $\triangle A D E$ and $\triangle B O C$ and then we will prove that the centers of these circles and the point $X$ are collinear, which is enough for proving that the circles are tangent to each other.
In this proof we will use the notation $(M N P)$ to denote the circumcircle of the triangle $\triangle M N P$.
Obviously, the quadrilateral $A D X E$ is cyclic, and the circle $(D A E)$ has $[A X]$ as diameter. (1)
Let $I$ be the incenter of triangle $A B C$. So, the point $I$ lies on the segment $[A X]$ (2), and the quadrilateral $X B I C$ is cyclic because $I C \perp X C$ and $I B \perp X B$. So, the circle (BIC) has $[I X]$ as diameter.
Finally, $m(\widehat{B I C})=90^{\circ}+\frac{1}{2} m(\widehat{B A C})=120^{\circ}$ and $m(\widehat{B O C})=2 m(\widehat{B A C})=120^{\circ}$.
So, the quadrilateral $B O I C$ is cyclic and the circle $(B O C)$ has $[I X]$ as diameter. (3)
(1), (2), (3) imply the conclusion.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 107 |
G3. A trapezoid $A B C D(A B \| C D, A B>C D)$ is circumscribed. The incircle of triangle $A B C$ touches the lines $A B$ and $A C$ at $M$ and $N$, respectively. Prove that the incenter of the trapezoid lies on the line $M N$.
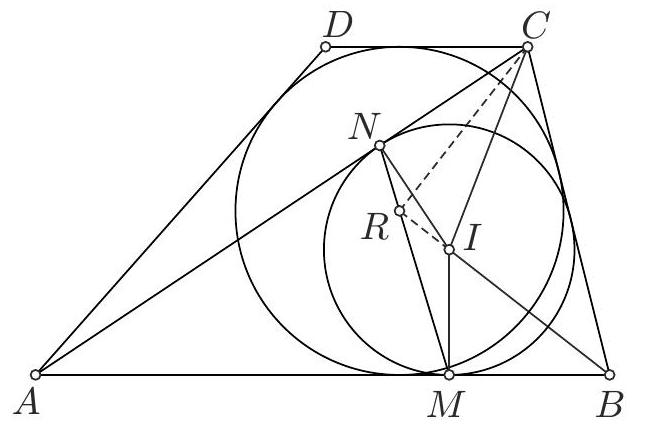
|
Solution. Let $I$ be the incenter of triangle $A B C$ and $R$ be the common point of the lines $B I$ and $M N$. Since
$$
m(\widehat{A N M})=90^{\circ}-\frac{1}{2} m(\widehat{M A N}) \quad \text { and } \quad m(\widehat{B I C})=90^{\circ}+\frac{1}{2} m(\widehat{M A N})
$$
the quadrilateral $I R N C$ is cyclic.
It follows that $m(\widehat{B R C})=90^{\circ}$ and therefore
$$
m(\widehat{B C R})=90^{\circ}-m(\widehat{C B R})=90^{\circ}-\frac{1}{2}\left(180^{\circ}-m(\widehat{B C D})\right)=\frac{1}{2} m(\widehat{B C D})
$$
So, $(C R$ is the angle bisector of $\widehat{D C B}$ and $R$ is the incenter of the trapezoid.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 108 |
G4. Let $A B C$ be an acute angled triangle whose shortest side is $[B C]$. Consider a variable point $P$ on the side $[B C]$, and let $D$ and $E$ be points on $(A B]$ and $(A C]$, respectively, such that $B D=B P$ and $C P=C E$. Prove that, as $P$ traces $[B C]$, the circumcircle of the triangle $A D E$ passes through a fixed point.
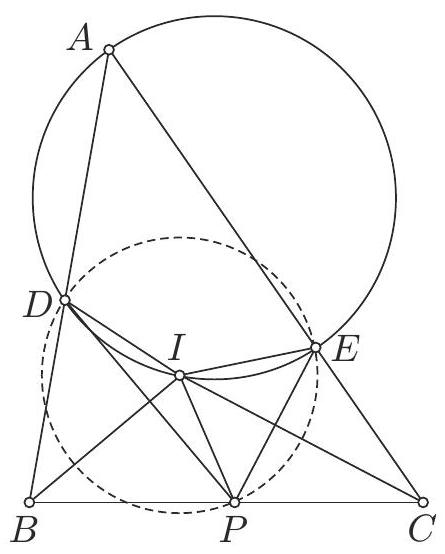
|
Solution. We claim that the fixed point is the center of the incircle of $A B C$.
Let $I$ be the center of the incircle of $A B C$. Since $B D=B P$ and $[B I$ is the bisector of $\widehat{D B P}$, the line $B I$ is the perpendicular bisector of $[D P]$. This yields $D I=P I$. Analogously we get $E I=P I$. So, the point $I$ is the circumcenter of the triangle $D E P$.
This means $m(\widehat{D I E})=2 m(\widehat{D P E})$.
On the other hand
$$
\begin{aligned}
m(\widehat{D P E}) & =180^{\circ}-m(\widehat{D P B})-m(\widehat{E P C}) \\
& =180^{\circ}-\left(90^{\circ}-\frac{1}{2} m(\widehat{D B P})\right)-\left(90^{\circ}-\frac{1}{2} m(\widehat{E C P})\right) \\
& =90^{\circ}-\frac{1}{2} m(\widehat{B A C})
\end{aligned}
$$
So, $m(\widehat{D I E})=2 m(\widehat{D P E})=180^{\circ}-m(\widehat{D A E})$, which means that the points $A, D, E$ and $I$ are cocyclic.
Remark. The fact that the incentre $I$ of the triangle $A B C$ is the required fixed point could be guessed by considering the two extremal positions of $P$. Thus, if $P=B$, then $D=D_{B}=B$ as well, and $C E=C E_{B}=B C$, so $m(\angle A E B)=m(\angle C)+m(\angle E B C)=$ $m(\angle C)+\frac{180^{\circ}-m(\angle C)}{2}=90^{\circ}+\frac{m(\angle C)}{2}=m(\angle A I B)$. Hence the points $A, E=E_{B}, I, D_{B}=B$ are cocyclic. Similarly, letting $P=C$, the points $A, D=D_{C}, I, E_{C}=C$ are cocyclic. Consequently, the circles $A D_{B} E_{B}$ and $A D_{C} E_{C}$ meet again at $I$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 109 |
G5. Let $A B C$ be an acute angled triangle with orthocenter $H$ and circumcenter $O$. Assume the circumcenter $X$ of $B H C$ lies on the circumcircle of $A B C$. Reflect $O$ across $X$ to obtain $O^{\prime}$, and let the lines $X H$ and $O^{\prime} A$ meet at $K$. Let $L, M$ and $N$ be the midpoints of $[X B],[X C]$ and $[B C]$, respectively. Prove that the points $K, L, M$ and $N$ are cocyclic.
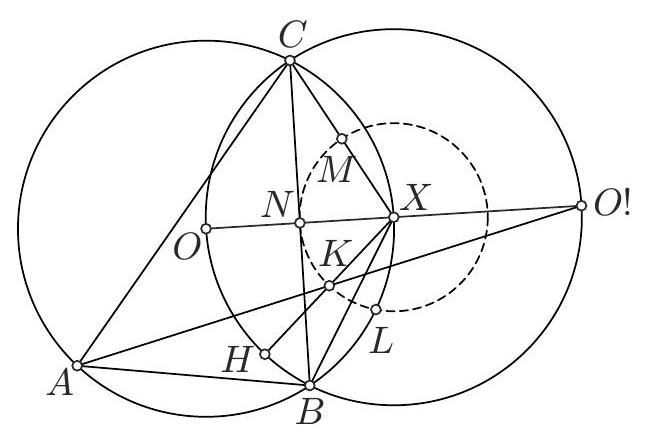
|
Solution. The circumcircles of $A B C$ and $B H C$ have the same radius. So, $X B=$ $X C=X H=X O=r$ (where $r$ is the radius of the circle $A B C$ ) and $O^{\prime}$ lies on $C(X, r)$. We conclude that $O X$ is the perpendicular bisector for $[B C]$. So, $B O X$ and $C O X$ are equilateral triangles.
It is known that $A H=2 O N=r$. So, $A H O^{\prime} X$ is parallelogram, and $X K=K H=r / 2$. Finally, $X L=X K=X N=X M=r / 2$. So, $K, L, M$ and $N$ lie on the circle $c(X, r / 2)$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 110 |
G6. Given an acute triangle $A B C$, erect triangles $A B D$ and $A C E$ externally, so that $m(\widehat{A D B})=m(\widehat{A E C})=90^{\circ}$ and $\widehat{B A D} \equiv \widehat{C A E}$. Let $A_{1} \in B C, B_{1} \in A C$ and $C_{1} \in A B$ be the feet of the altitudes of the triangle $A B C$, and let $K$ and $L$ be the midpoints of $\left[B C_{1}\right]$ and $\left[C B_{1}\right]$, respectively. Prove that the circumcenters of the triangles $A K L, A_{1} B_{1} C_{1}$ and $D E A_{1}$ are collinear.
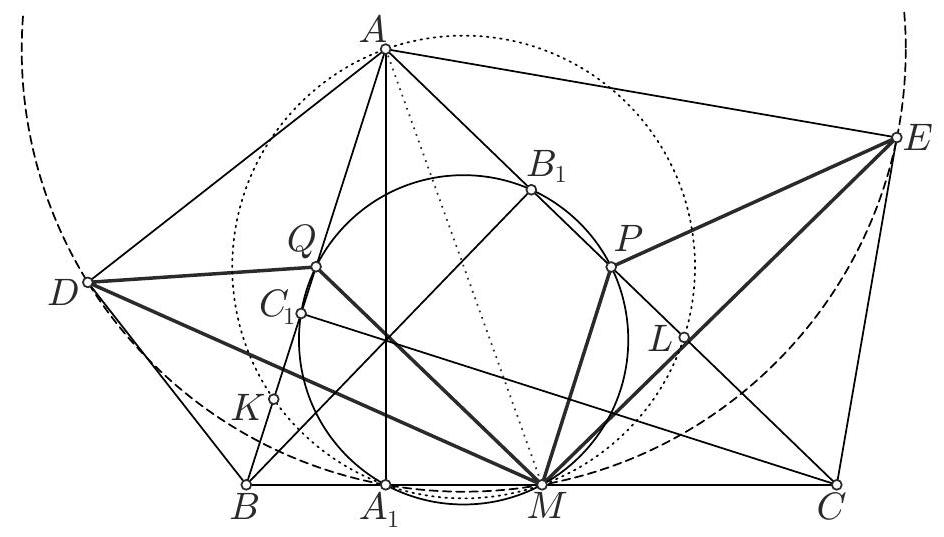
|
Solution. Let $M, P$ and $Q$ be the midpoints of $[B C],[C A]$ and $[A B]$, respectively.
The circumcircle of the triangle $A_{1} B_{1} C_{1}$ is the Euler's circle. So, the point $M$ lies on this circle.
It is enough to prove now that $\left[A_{1} M\right]$ is a common chord of the three circles $\left(A_{1} B_{1} C_{1}\right)$, $(A K L)$ and $\left(D E A_{1}\right)$.
The segments $[M K]$ and $[M L]$ are midlines for the triangles $B C C_{1}$ and $B C B_{1}$ respectively, hence $M K \| C C_{1} \perp A B$ and $M L \| B B_{1} \perp A C$. So, the circle $(A K L)$ has diameter $[A M]$ and therefore passes through $M$.
Finally, we prove that the quadrilateral $D A_{1} M E$ is cyclic.
From the cyclic quadrilaterals $A D B A_{1}$ and $A E C A_{1}, \widehat{A A_{1} D} \equiv \widehat{A B D}$ and $\widehat{A A_{1} E} \equiv \widehat{A C E} \equiv$ $\widehat{A B D}$, so $m\left(\widehat{D A_{1} E}\right)=2 m(\widehat{A B D})=180^{\circ}-2 m(\widehat{D A B})$.
We notice now that $D Q=A B / 2=M P, Q M=A C / 2=P E$ and
$$
\begin{aligned}
& m(\widehat{D Q M})=m(\widehat{D Q B})+m(\widehat{B Q M})=2 m(\widehat{D A B})+m(\widehat{B A C}) \\
& m(\widehat{E P M})=m(\widehat{E P C})+m(\widehat{C P M})=2 m(\widehat{E A C})+m(\widehat{C A B})
\end{aligned}
$$
so $\triangle M P E \equiv \triangle D Q M$ (S.A.S.). This leads to $m(\widehat{D M E})=m(\widehat{D M Q})+m(Q M P)+$ $m(P M E)=m(\widehat{D M Q})+m(B Q M)+m(Q D M)=180^{\circ}-m(\widehat{D Q B})=180^{\circ}-2 m(\widehat{D A B})$. Since $m\left(\widehat{D A_{1} E}\right)=m(\widehat{D M E})$, the quadrilateral $D A_{1} M E$ is cyclic.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 111 |
G7. Let $[A B]$ be a chord of a circle $(c)$ centered at $O$, and let $K$ be a point on the segment $(A B)$ such that $A K<B K$. Two circles through $K$, internally tangent to (c) at $A$ and $B$, respectively, meet again at $L$. Let $P$ be one of the points of intersection of the line $K L$ and the circle (c), and let the lines $A B$ and $L O$ meet at $M$. Prove that the line $M P$ is tangent to the circle $(c)$.
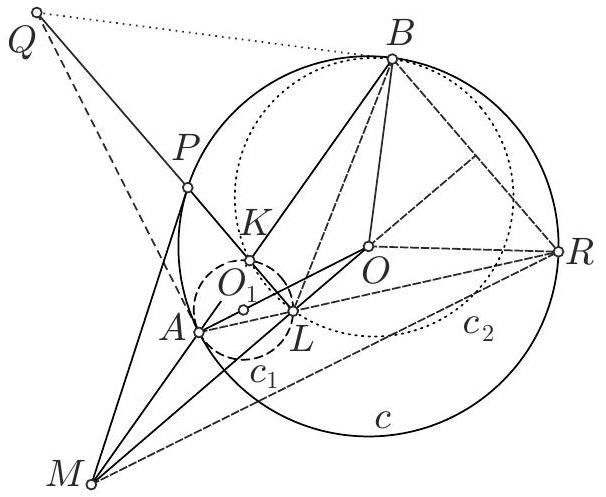
|
Solution. Let $\left(c_{1}\right)$ and $\left(c_{2}\right)$ be circles through $K$, internally tangent to (c) at $A$ and $B$, respectively, and meeting again at $L$, and let the common tangent to $\left(c_{1}\right)$ and $(c)$ meet the common tangent to $\left(c_{2}\right)$ and $(c)$ at $Q$. Then the point $Q$ is the radical center of the circles $\left(c_{1}\right),\left(c_{2}\right)$ and $(c)$, and the line $K L$ passes through $Q$.
We have $m(\widehat{Q L B})=m(\widehat{Q B K})=m(\widehat{Q B A})=\frac{1}{2} m(\overparen{B A})=m(\widehat{Q O B})$. So, the quadrilateral $O B Q L$ is cyclic. We conclude that $m(\widehat{Q L O})=90^{\circ}$ and the points $O, B, Q, A$ and $L$ are cocyclic on a circle $(k)$.
In the sequel, we will denote $\mathcal{P}_{\omega}(X)$ the power of the point $X$ with respect of the circle $\omega$. The first continuation.
From $M O^{2}-O P^{2}=\mathcal{P}_{c}(M)=M A \cdot M B=\mathcal{P}_{k}(M)=M L \cdot M O=(M O-O L) \cdot M O=$ $M O^{2}-O L \cdot M O$ follows that $O P^{2}=O L \cdot O M$. Since $P L \perp O M$, this shows that the triangle $M P O$ is right at point $P$. Thus, the line $M P$ is tangent to the circle (c).
The second continuation.
Let $R \in(c)$ be so that $B R \perp M O$. The triangle $L B R$ is isosceles with $L B=L R$, so $\widehat{O L R} \equiv \widehat{O L B} \equiv \widehat{O Q B} \equiv \widehat{O Q A} \equiv \widehat{M L A}$. We conclude that the points $A, L$ and $R$ are collinear.
Now $m(\widehat{A M R})+m(\widehat{A O R})=m(\widehat{A M R})+2 m(\widehat{A B R})=m(\widehat{A M R})+m(\widehat{A B R})+m(\widehat{M R B})=$ $180^{\circ}$, since the triangle $M B R$ is isosceles. So, the quadrilateral $M A O R$ is cyclic.
This yields $L M \cdot L O=-\mathcal{P}_{(\text {MAOR })}(L)=L A \cdot L R=-\mathcal{P}_{c}(L)=L P^{2}$, which as above, shows that $O P \perp P M$.
The third continuation.
$\widehat{K L A} \equiv \widehat{K A Q} \equiv \widehat{K L B}$ and $m(\widehat{M L K})=90^{\circ}$ show that $[L K$ and $[L M$ are the internal and external bisectors af the angle $\widehat{A L B}$, so $(M, K)$ and $(A, B)$ are harmonic conjugates. So, $L K$ is the polar line of $M$ in the circle $(c)$.
## Chapter 4
## Number Theory
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 112 |
C 2. Viktor and Natalia bought 2020 buckets of ice-cream and want to organize a degustation schedule with 2020 rounds such that:
- In every round, each one of them tries 1 ice-cream, and those 2 ice-creams tried in a single round are different from each other.
- At the end of the 2020 rounds, each one of them has tried each ice-cream exactly once.
We will call a degustation schedule fair if the number of ice-creams that were tried by Viktor before Natalia is equal to the number of ice creams tried by Natalia before Viktor.
Prove that the number of fair schedules is strictly larger than $2020!\left(2^{1010}+(1010!)^{2}\right)$.
|
Solution. If we fix the order in which Natalia tries the ice-creams, we may consider 2 types of fair schedules:
1) Her last 1010 ice-creams get assigned as Viktor's first 1010 ice-creams, and vice versa: Viktor's first 1010 ice-creams are assigned as Natalia's last 1010 ice-creams. This generates (1010!) $)^{2}$ distinct fair schedules by permuting the ice-creams within each group.
2) We divide all ice-creams into disjoint groups of 4 , and in each group we swap the first 2 ice-creams with the last 2 , which gives us $\left((2!)^{2}\right)^{504}=2^{1010}$ distinct schedules.
Now, to make the inequality strict, we consider 1 more schedule like 2 ), but with groups of 2 ice-creams instead of 4 .
|
proof
|
Combinatorics
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 113 |
G 1. Let $\triangle A B C$ be an acute triangle. The line through $A$ perpendicular to $B C$ intersects $B C$ at $D$. Let $E$ be the midpoint of $A D$ and $\omega$ the the circle with center $E$ and radius equal to $A E$. The line $B E$ intersects $\omega$ at a point $X$ such that $X$ and $B$ are not on the same side of $A D$ and the line $C E$ intersects $\omega$ at a point $Y$ such that $C$ and $Y$ are not on the same side of $A D$. If both of the intersection points of the circumcircles of $\triangle B D X$ and $\triangle C D Y$ lie on the line $A D$, prove that $A B=A C$.
|
Solution. Denote by $s$ the line $A D$. Let $T$ be the second intersection point of the circumcircles of $\triangle B D X$ and $\triangle C D Y$. Then $T$ is on the line $s$. Note that $C D Y T$ and $B D X T$ are cyclic. Using this and the fact that $A D$ is perpendicular to $B C$ we obtain:
$$
\angle T Y E=\angle T Y C=\angle T D C=90^{\circ}
$$
This means that $E Y$ is perpendicular to $T Y$, so $T Y$ must be tangent to $\omega$. We similarly show that $T X$ is tangent to $\omega$. Thus, $T X$ and $T Y$ are tangents from $T$ to $\omega$ which implies that $s$ is the perpendicular bisector of the segment $X Y$. Now denote by $\sigma$ the reflection of the plane with respect to $s$. Then the points $X$ and $Y$ are symmetric with respect to $s$, so $\sigma(X)=Y$. Also note that $\sigma(E)=E$, because $E$ is on $s$. Using the fact that $B C$ is perpendicular to $s$, we see that $B C$ is the reflection image of itself with respect to $s$. Now note that $B$ is the intersection point of the lines $E X$ and $B C$. This means that the image of $B$ is the intersection point of the lines $\sigma(E X)=E Y$ and $\sigma(B C)=B C$, which is $C$. From here we see that $\sigma(B)=C$, so $s$ is the perpendicular bisector of $B C$, which is what we needed to prove.
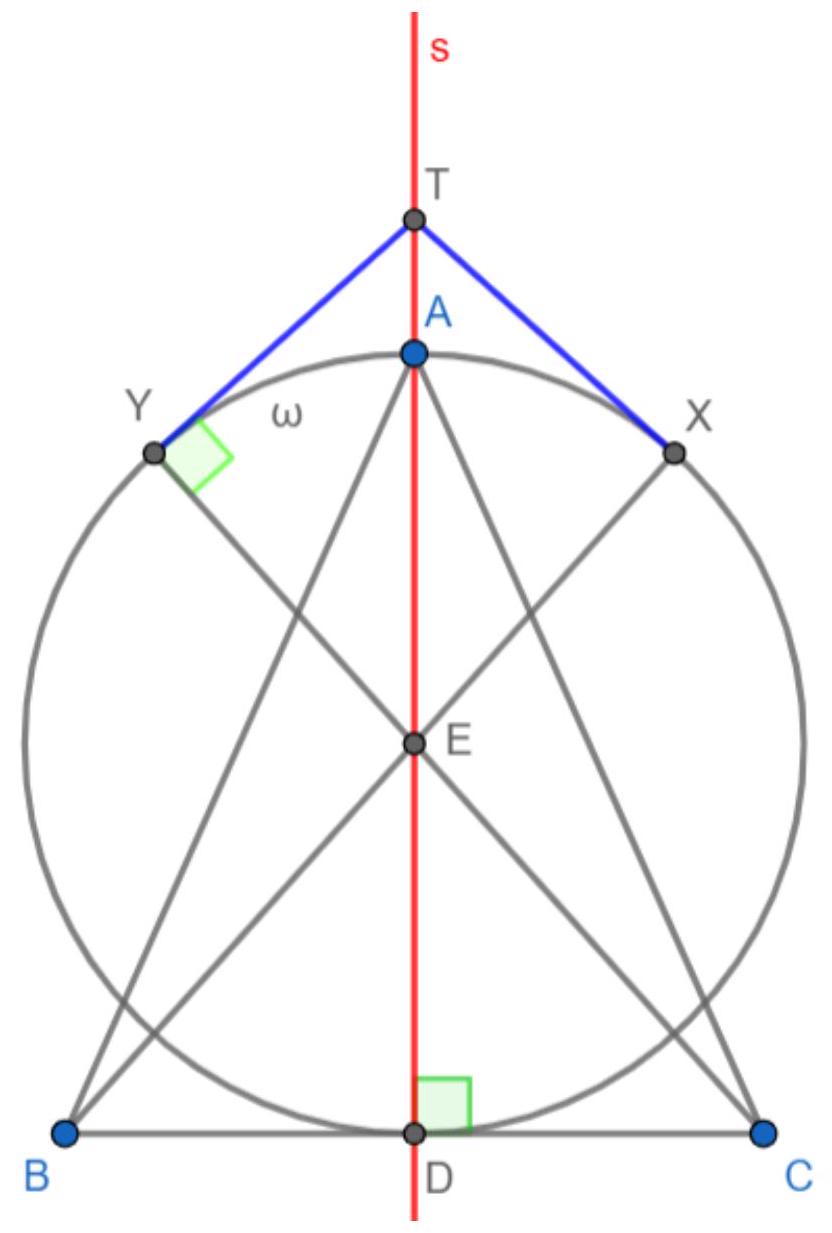
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 114 |
End of preview. Expand
in Data Studio
NuminaMath-1.5-proofs-only-strict
A strictly filtered version of the NuminaMath-1.5-proofs-only dataset, containing ONLY validated mathematical proof problems.
📊 Filtering Results
Original dataset: Numina1.5 -> filter for proofs -> 110,998 rows
Filters applied:
- ✓ Kept rows where
answer = "proof"(proof problems only) - ✓ Kept rows where
solution_is_valid = "Yes" - ✓ Kept rows where
problem_is_valid = "Yes" - ✓ Dropped validation columns after filtering
- ✓ Kept rows where
Filtered dataset: 58,088 rows (removed 52,910 rows)
📦 Dataset
- Columns preserved:
problem- The mathematical problem statement requiring a proofsolution- Step-by-step proof/solutionanswer- Always "proof" (filtered to contain only proof problems)problem_type- Type of mathematical problemquestion_type- Question format/stylesource- Original source of the problemsynthetic- Whether the problem is synthetically generatedsource_dataset- Source dataset identifiersource_split- Dataset split (train/test/val)
This strict version contains only validated mathematical proof problems, perfect for training models on formal mathematical reasoning and proof generation.
- Downloads last month
- 100